GPIGuide - Correlation: Difference between revisions
No edit summary |
No edit summary |
||
| Line 80: | Line 80: | ||
A tag value greater than 0 enables correlation on the subsequent primitives, but only if the segment ID is greater than 0 as well. The data returned from each correlation consists of a set of segment-tag pairs. The reason for this pairing is that a single segment can draw objects in several locations. By adding identifiers within the segment, an application has a more exact description of what has intersected the pick aperture. | A tag value greater than 0 enables correlation on the subsequent primitives, but only if the segment ID is greater than 0 as well. The data returned from each correlation consists of a set of segment-tag pairs. The reason for this pairing is that a single segment can draw objects in several locations. By adding identifiers within the segment, an application has a more exact description of what has intersected the pick aperture. | ||
For simple chained segments, each unique segment-tag pair within the pick aperture is known as a ''hit''. If two or more primitives in the pick aperture have the same tag, they are considered a single hit. Hits for called segments differ slightly and are described in [[#The lMaxDepth Input Parameter]]. | For simple chained segments, each unique segment-tag pair within the pick aperture is known as a ''hit''. If two or more primitives in the pick aperture have the same tag, they are considered a single hit. Hits for called segments differ slightly and are described in [[#The lMaxDepth Input Parameter|The lMaxDepth Input Parameter]]. | ||
==== Correlation Functions for Retained Graphics ==== | ==== Correlation Functions for Retained Graphics ==== | ||
Latest revision as of 18:21, 9 May 2025
Reprint Courtesy of International Business Machines Corporation, © International Business Machines Corporation
Correlation
Correlation is the process of determining which primitives, if any, are contained in an area of interest. The process for nonretained graphics is very different from the process for retained graphics. The following topics are related to the information in this chapter:
- Presentation spaces
- Coordinate spaces and transformations
- Editing retained graphics and graphics segments
About Correlation
When you want to select an area of interest on the screen, you usually move the pointer to the applicable point and signal (by clicking a mouse, for example) that this is the object you want. This selection process most commonly is used for graphic applications. For example, your application could permit a user to select an object, then change its color. Correlation, however, can also be used in nongraphic applications. For example, your application could model the operation of a calculator and permit a user to select numbers for mathematical operations.
The area of interest is defined by the operating system as a small rectangle, centered on the (x,y) coordinate position, that has been sent to the application. The virtual rectangle the application generates is known as the pick aperture. The following figure shows an example of a pick aperture. 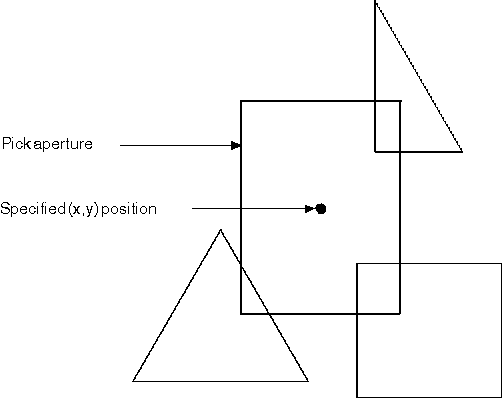
The Pick Aperture
The process of determining what lies in the pick aperture differs between nonretained and retained graphics. For nonretained graphics, the presentation space must be put in a state that supports correlation before the primitives are drawn. Then correlation is performed while the primitives are being drawn. For retained graphics, the segments that contain the graphics can be replayed, permitting correlation after the primitives are drawn.
Note: The necessity to correlate graphics can usually be predicted. Therefore you can plan for it when designing applications. However, this does not mean that you have to create retained (rather than nonretained) graphic segments. The decision to retain graphics is dependent on several considerations of which correlation is only one.
Correlating Nonretained Graphics
For the purposes of correlation, nonretained graphics are those graphics that are being correlated during the drawing process. Nonretained graphics can exist in nonretained graphic segments or completely outside any segment structure. Primitives outside segments are detectable when the applicable draw control is set.
Nonretained graphics, inside a segment bracket, can be created in either draw or draw-and-retain modes. If created in draw-and-retain mode, a segment, at first, is considered nonretained while the primitives in the segment are being drawn; then it is considered retained. To be correlated, nonretained segments must have unique, nonzero identifiers, and must be defined as detectable. The primitives within these segments can be tagged just as primitives in retained segments are. However, the tags do not influence the correlation process for nonretained graphics.
To get correlation data from the drawing of nonretained graphics, three steps must be performed - after creation of the presentation space but before drawing the primitives:
1. Call GpiSetDrawControl to switch on the correlation flag (DCTL_CORRELATE, DCTL_ON). 2. Call GpiSetPickApertureSize, if necessary, to change the size of the pick aperture. 3. Call GpiSetPickAperturePosition, if necessary, to explicitly position the aperture. As input to this function, you provide the coordinate position on which the pick aperture is to be centered, using presentation page coordinates.
Correlation is performed for the following functions:
- Individual primitive-drawing requests, for example, GpiBox
- GpiPutData
- GpiElement
- GpiPlayMetaFile
Correlation is never performed for GpiErase.
You detect correlation hits by examining the returned values from the GPI functions. If GpiLine, for example, draws a line that intersects the pick aperture, it returns a value of GPI_HITS to indicate a correlation hit. If the line does not intersect the pick aperture, GpiLine returns a value of GPI_OK, to indicate the successful drawing of a line without a correlation hit. GpiLine returns a value of GPI_ERROR if an error is detected.
If the line intersects the pick aperture, a correlation hit is returned even if the line style is LINETYPE_INVISIBLE. For other primitives, if the object is drawn in outline mode, a correlation hit is returned only if the pick aperture intersects the boundary. If the object is in fill mode, a correlation hit is returned if the pick aperture intersects or lies within the boundary.
The following figure is an example of primitives intersecting the pick aperture. 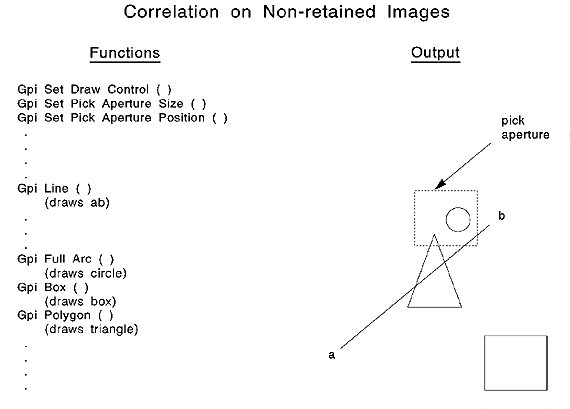
Correlating Nonretained Graphics
Each GPI function whose output intersects the pick aperture returns a hit (GPI_HIT). GpiBox, whose output does not intersect the pick aperture, returns GPI_OK.
Correlating Retained Graphics
The information in a retained graphic segment can be redrawn; therefore, setting up an environment for correlation is not necessary. Correlation on retained segments is processed through segment IDs and tags throughout the segments.
For any retained segment to be a candidate for correlation, the following must be done:
1. Call GpiOpenSegment with a unique, nonzero identifier. 2. Call GpiSetSegmentAttrs with the following settings:
a. ATTR_DETECTABLE switched ON b. ATTR_DYNAMIC left OFF (default), unless the segment is unchained and, therefore, drawn non-dynamically c. ATTR_PROP_DETECTABLE left ON (default), in any segment that calls the candidate segment
3. Call GpiSetTag at appropriate locations within the segment.
Note: The preceding is the recommended method. However, an application still can receive correlation data about invisible segments.
Tagging Primitives within a Segment
GpiSetTag inserts a long integer value, called a tag, at the current element pointer position. The tag becomes a segment element, which serves as an identifier for the primitives that follow until the next tag is issued. Tags also are called pick tags or pick identifiers. Typically, applications assign tags only to elements that correspond to primitives. You can determine the value of the last tag assigned to an element using GpiQueryTag.
Note: Tags are used only in correlation. They are not used in the chaining or calling of segments, nor do they cause or modify output.
The long integer value of the tag is 0 by default. However, a 0 value makes the subsequent primitives undetectable. An application can use this effect to make some parts of a segment detectable and other parts of it non-detectable. If you know that this capability is unnecessary, you can change the default tag value using GpiSetDefTag.
The tag you specify becomes the current tag, and it applies to all subsequent primitives until you next call GpiSetTag. The tag can be considered one of the attributes of the primitive and therefore affected by the current attribute mode. In AM_PRESERVE mode, it is stored on the LIFO stack and can be recalled with GpiPop. Tags cannot be inserted between a GpiBeginArea and GpiEndArea area bracket. All primitives within an area have the same tag.
A tag value greater than 0 enables correlation on the subsequent primitives, but only if the segment ID is greater than 0 as well. The data returned from each correlation consists of a set of segment-tag pairs. The reason for this pairing is that a single segment can draw objects in several locations. By adding identifiers within the segment, an application has a more exact description of what has intersected the pick aperture.
For simple chained segments, each unique segment-tag pair within the pick aperture is known as a hit. If two or more primitives in the pick aperture have the same tag, they are considered a single hit. Hits for called segments differ slightly and are described in The lMaxDepth Input Parameter.
Correlation Functions for Retained Graphics
The PM has three different functions that enable you to correlate a uniquely identified retained segment.
| Function | Description |
|---|---|
| GpiCorrelateSegment | Permits correlation on a single segment. |
| GpiCorrelateFrom | Permits correlation on a range of segments from a segment chain. |
| GpiCorrelateChain | Permits correlation on the entire segment chain. |
For nonretained graphics, the correlation hits are returned by the actual drawing commands. For retained graphics, the correlation hits are returned by the three correlation functions listed above.
The size of the pick aperture is set using GpiSetPickApertureSize, just as with nonretained graphics. However, the coordinate position on which the pick aperture is centered usually is obtained from operator input, for example, from a WM_BUTTON1DOWN message, instead of from GpiSetPickAperturePosition.
After the graphics orders that create pictures are stored in retained segments, the pictures can be re-created by your application with the various GpiDraw... functions. Then the user can view the pictures, if the output is directed to a screen for example. After the user selects an area of interest, a GpiCorrelate... function redraws the picture internally to determine just what intersects the pick aperture. The user does not see the re-creation. A standard order of functions within your application would be:
- GpiDraw...
- GpiSetPickApertureSize
- GpiCorrelate...
The Correlation Input Parameters
There is only one segment chain per presentation space. Therefore GpiCorrelateChain needs the presentation space handle as input. The segment correlation functions need both the presentation space handle and the segment IDs.
All three correlation functions require the following as input:
- Correlation attribute type
- Maximum number of hits
- Number of segment-tag pairs to be returned for a single hit, called the pair depth.
The lType Input Parameter
The two classifications of segments upon which you can request correlation are the following:
- Segments that have been defined as both detectable and visible
- All nonzero segments, regardless of their detectability and visibility attributes
The lMaxHits Input Parameter
The correlation functions return the number of hits made on the retained segments. The following figure is an example of a line intersecting the pick aperture. 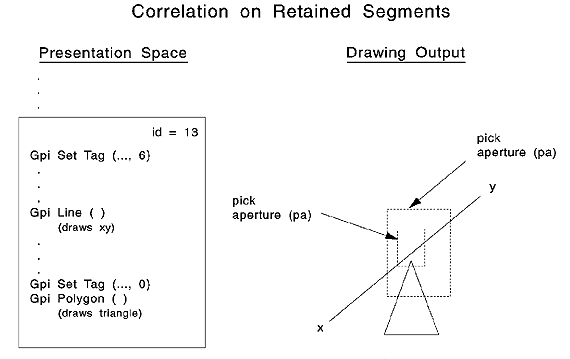
Retained Segment Correlation with One Hit
The intersection of a unique segment-identified and -tagged primitive with the pick aperture (pa) produces one hit. If the pick aperture size were increased, there still would be only 1 hit. The triangle produces no hit because its tag is 0.
The following figure is an example of multiple primitives intersecting the pick aperture. 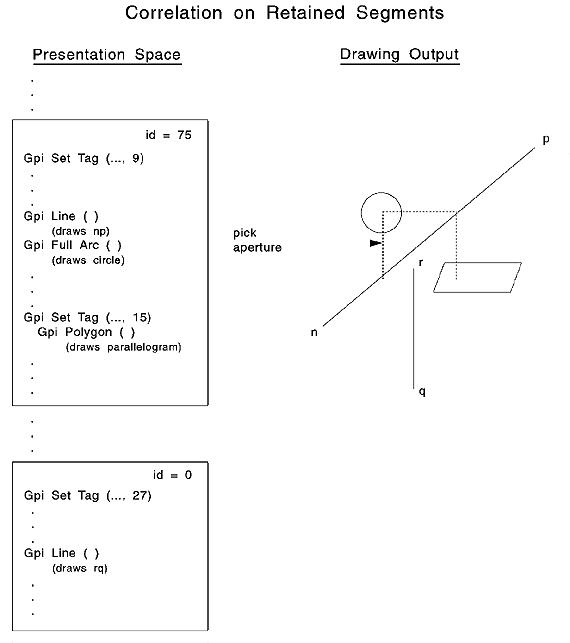
Retained Segment Correlation with Multiple Hits
Four separate primitives intersect the pick aperture; however, since two primitives share the same tag, and one primitive has a segment ID of 0, there are only two hits.
Your application can set a limit on the number of hits to return from a correlation function. The maximum-number-of-hits parameter influences the size of the array created to handle the segment-tag pair returned for each hit. By comparing the maximum number desired to the actual number of hits, your application can determine whether all hits are accounted for. The following figure shows an example of the alSegTag data structure that contains the segment-tag pairs for the previous figure. 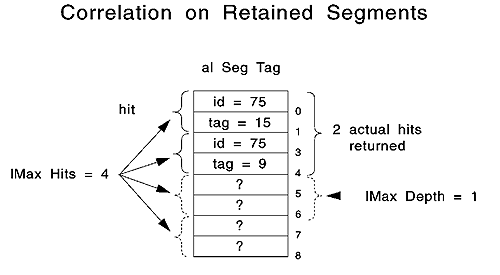
alSegTag Data Structure
As shown in the previous figure, the identifier-tag pairs are returned to the application in the reverse order of their occurrence on the segment chain. That is, the highest priority segment is returned first. Therefore, the application can identify the topmost segment, which is the segment most likely to have been picked.
The lMaxDepth Input Parameter
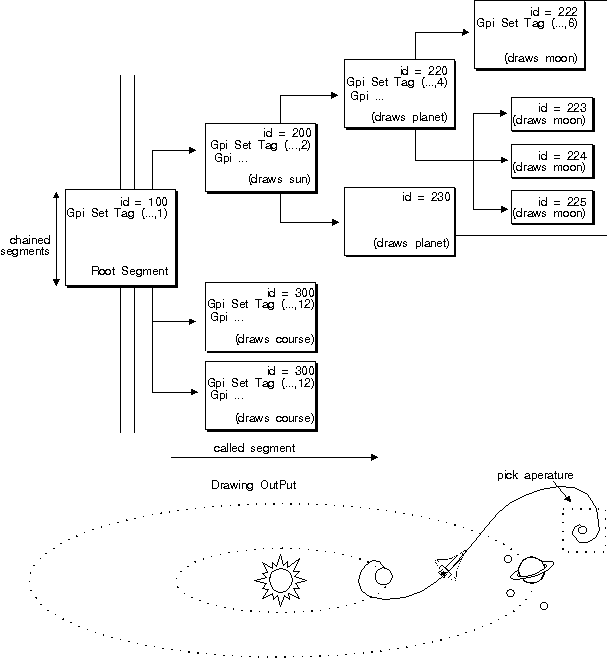
When a called segment is picked, correlation data is returned also for all segments above it in the hierarchy, up to and including the root segment. The following figure is an example of a picture drawn from a complex segment chain with called segments.
Multiple Hits from a Called Segment
Two separate items, called from different portions of the segment chain, intersect the pick aperture. Each has a unique segment identifier and tag, so there are two hits.
For called segments, the group of segment-tag pairs constitutes a single hit. You can limit the number of segment and tag pairs returned for each hit using the maximum depth parameter, just as you can limit the total number of hits returned to you using the maximum number of hits parameter. The following figure shows two examples of the alSegTag data structure from the previous figure, for two different lMaxDepth values.
┌─ ┌────────┐ ──┐ ┌─── ┌────────┐ ──┐
│ │id = 300│ 0│ │ │id = 300│ 0│
│ ├────────┤ │ │ ├────────┤ │
│ │tag = 12│ 1│ │ │tag = 12│ 1│
┌─────┤ ├────────┤ │ │ ├────────┤ │
│ │ │id = 100│ 2│ │ │id = 100│ 2│
│ │ ├────────┤ │ │ ├────────┤ │
│ │ │tag = 1 │ 3│ 2 actual │ │tag = 1 │ 3│
│ ╞═ ├────────┤ ├── hits ──┤ ├────────┤ ├────┐
│ │ │id = 222│ 4│ returned │ │ 0 │ 4│ │
│ │ ├────────┤ │ │ ├────────┤ │ │
IMax │ │tag = 6 │ 5│ │ │ 0 │ 5│ │
hits─────┤ ├────────┤ │ │ ├────────┤ │ │
= 3 │ │id = 220│ 6│ │ │ 0 │ 6│ │
│ │ ├────────┤ │ │ ├────────┤ │ │
│ │ │tag = 4 │ 7│ │ │ 0 │ 7│ │
│ ╞═ ├────────┤ ══╡ │ ┌─ ├────────┤ ══╡ │
│ │ │ ? │ 8│ │ │ │id = 222│ 8│ │
│ │ ├────────┤ │ │ │ ├────────┤ │ │
│ │ │ ? │ 9│ IMax │ │ │tag = 6 │ 9│ │
└─────┤ ├────────┤ ├─ Depth │ │ ├────────┤ │ │
│ │ ? │ 10│ = 2 │ │ │id = 220│ 10│ │
│ ├────────┤ │ │ │ ├────────┤ │ │
│ │ ? │ 11│ IMax │ │ │tag = 4 │ 11│ IMax
└─ └────────┘ ──┘ Depth│─┤ ├────────┤ ├─ hits
= 4 │ │ │id = 200│ 12│ = 3
│ │ ├────────┤ │ │
│ │ │tag = 2 │ 13│ │
│ │ ├────────┤ │ │
│ │ │id = 100│ 14│ │
│ │ ├────────┤ │ │
│ │ │tag = 1 │ 15│ │
└─└─ ├────────┤ ══╡ │
│ ? │ 16│ │
├────────┤ │ │
│ ? │ 17│ │
├────────┤ │ │
│ ? │ 18│ │
├────────┤ │ │
│ ? │ 19│ │
├────────┤ ├────┘
│ ? │ 20│
├────────┤ │
│ ? │ 21│
├────────┤ │
│ ? │ 22│
├────────┤ │
│ ? │ 23│
└────────┘ ──┘
alSegTag Data Structure for Different lMaxDepth Values
Unused segment-tag pairs for actual hits are set to 0 in the alSegTag array.
There are two major reasons for the PM to provide this capacity. The first is the consideration of application storage. If your application is a graphics package, for example, providing extensive design capabilities to an end user, the user's drawing may be very complex with 10 or more levels of segment calling. The data returned from a single hit could require an alSegTag array so large the data overruns the application storage you had reserved. By setting a maximum calling depth, your application can reserve the correct amount of storage.
The second consideration is the knowledge that your application's user is interested only in a certain level of calling depth. Many users will be interested only in the topmost called segment, because it usually is the segment containing the functions that performs the actual drawing.
Pick Aperture
Your application determines the size of the pick aperture using GpiQueryPickApertureSize, and determines the page space coordinates of the center of the aperture with GpiQueryPickAperturePosition.
Because your objective is to retrieve a single detectable object for each correlation operation, you have to obtain a balance between the number of detectable objects in a picture and the size of the pick aperture. The more detectable objects you define, the smaller the pick aperture must be to return a manageable amount of information to the application. However, the pick aperture usually is not a 1 pel-by-1 pel rectangle. A larger rectangle makes better sense because the pick aperture can be difficult to hit with a single pel; but a larger sampling area, for example 4 pels-by-4 pels, increases the probability of an intersection between a lighted pel and the pick aperture.
The pick aperture can be specified in any of the units available to the presentation space. However, the type of unit must be identical to the type specified for the presentation page. The default size of the pick aperture is square, with sides equal to the default character cell height.
Using Correlation
This section explains how to perform correlation on the graphics associated with a segment.
The following figure shows how to set the pick aperture size with GpiSetPickAperture and correlate the segment chain with GpiCorrelateChain, passing it the pick-aperture position as the third argument. The functions use the psizlPick and pptlPick arguments to set the aperture size and position the aperture center. The correlation is performed on visible and detectable segments only (PICKSEL_VISIBLE). GpiCorrelateChain copies any segment-tag pairs to the buffer pointed to by alSegTag and returns the count of hits detected.
#define INCL_GPICORRELATION
#include <os2.h>
LONG fncCORL01 (HPS hps, PSIZEL psizlPick, PPOINTL pptlPick,
LONG lMaxHits, LONG lMaxDepth, PLONG alSegTag)
{
LONG cHits;
GpiSetPickApertureSize(hps, PICKAP_REC, psizlPick);
/* Set the pick aperture. */
cHits = GpiCorrelateChain(hps, PICKSEL_VISIBLE, pptlPick,
lMaxHits, lMaxDepth, alSegTag);
/* Correlate the hits. */
return (cHits); /* Return count of hits. */
} /* fncCORL01 */