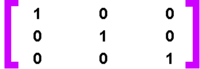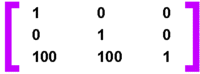Using Transforms in your PM Graphics Applications: Difference between revisions
Created page with "by Kelvin R. Lawrence The OS/2 Graphical Programming Interface (GPI) contains many powerful features that let you construct and manipulate graphical shapes. However, many pr..." |
No edit summary |
||
| Line 1: | Line 1: | ||
by [[Kelvin R. Lawrence]] | ''by [[Kelvin R. Lawrence]]'' | ||
The OS/2 Graphical Programming Interface (GPI) contains many powerful features that let you construct and manipulate graphical shapes. However, many programmers have avoided using these features in their applications. There is a myth, it seems, that the GPI is hard to program to and hard to learn. In reality, this is not the case. This article shows you how the GPI lets you work with its transformation matrices and describes how to setup simple transformations to change the way picture components or whole pictures are drawn. | The OS/2 Graphical Programming Interface (GPI) contains many powerful features that let you construct and manipulate graphical shapes. However, many programmers have avoided using these features in their applications. There is a myth, it seems, that the GPI is hard to program to and hard to learn. In reality, this is not the case. This article shows you how the GPI lets you work with its transformation matrices and describes how to setup simple transformations to change the way picture components or whole pictures are drawn. | ||
This article; however, describes some of the effects you can achieve by using just the model transform. | This article; however, describes some of the effects you can achieve by using just the ''model transform''. | ||
==The Model Transform== | ==The Model Transform== | ||
The model transform is a general purpose ''work-horse'' transformation that lets you adjust the way a shape is drawn in a number of ways. One or more of the following effects can be achieved: | |||
* Translation: Move the shape to a new position | |||
* Rotation: Rotate the shape by a number of degrees | |||
* Scaling: Make the shape bigger or smaller | |||
* Reflection: Draw the mirror image of a shape | |||
* Shearing: Add a shear to the shape | |||
[[Image:Trans-PM-Fig1.gif|400px]] | |||
[[Image:Trans-PM-Fig1.gif]] | |||
Figure 1. Different Effects Using the Model Transform | Figure 1. Different Effects Using the Model Transform | ||
Manipulate each transform by creating and modifying a MATRIXLF structure as defined in the PMGPI.H header file in The Developer's Toolkit for OS/2 2.1 . | Manipulate each transform by creating and modifying a <tt>MATRIXLF</tt> structure as defined in the PMGPI.H header file in The Developer's Toolkit for OS/2 2.1. | ||
The MATRIXLF structure is defined in C as: | The MATRIXLF structure is defined in C as: | ||
<code> | |||
typedef struct _MATRIXLF { /* matlf */ | typedef struct _MATRIXLF { /* matlf */ | ||
FIXED fxM11; | |||
FIXED fxM12; | |||
LONG lM13; | |||
FIXED fxM21; | |||
FIXED fxM22; | |||
LONG lM23; | |||
LONG lM31; | |||
LONG lM32; | |||
LONG lM33; | |||
} MATRIXLF; | } MATRIXLF; | ||
</code> | |||
In more traditional matrix notation, think of the MATRIXLF structure as a three by three matrix as follows: | In more traditional matrix notation, think of the MATRIXLF structure as a three by three matrix as follows: | ||
[[Image:Trans-PM-Fig2.gif]] | [[Image:Trans-PM-Fig2.gif|200px]] | ||
To get the new value of a point about to be drawn, multiply the (x,y) coordinate against a transform matrix as follows: | To get the new value of a point about to be drawn, multiply the (x,y) coordinate against a transform matrix as follows: | ||
[[Image:Trans-PM-Fig3.gif]] | [[Image:Trans-PM-Fig3.gif|300px]] | ||
As shown in Figure 1, you can combine the different elements of the transformation matrix (MATRIXLF) structure in various ways to achieve various effects: | As shown in ''Figure 1'', you can combine the different elements of the transformation matrix (MATRIXLF) structure in various ways to achieve various effects: | ||
If you are working with a presentation space created so that the page units are defined as pels, then, by default, the GPI initializes the model transform to identity. In other words, it has no effect on anything. If you multiply an (x,y) coordinate against the transform it remains unchanged. However, if you are working in page units other than pels, the graphics subsystem initializes the model transform to match the page units that the application uses. Given that the GPI uses the lM31 and lM32 elements of the transformation matrix tructure for translating points, the following example illustrates the previous points. | If you are working with a presentation space created so that the page units are defined as pels, then, by default, the GPI initializes the model transform to ''identity''. In other words, it has no effect on anything. If you multiply an (x,y) coordinate against the transform it remains unchanged. However, if you are working in page units other than pels, the graphics subsystem initializes the model transform to match the page units that the application uses. Given that the GPI uses the lM31 and lM32 elements of the transformation matrix tructure for translating points, the following example illustrates the previous points. | ||
Assuming we are working in pels and that we have not yet adjusted the model transform then it will be initialized as an identity matrix as follows: | Assuming we are working in pels and that we have not yet adjusted the model transform then it will be initialized as an ''identity'' matrix as follows: | ||
[[Image:Trans-PM-Fig4.gif]] | [[Image:Trans-PM-Fig4.gif|200px]] | ||
Assuming we wanted a translation of 100 pels in both the x and y directions to be applied to all subsequent drawing operations, we can set up the lM31 and lM32 elements to reflect this as follows: | Assuming we wanted a translation of 100 pels in both the x and y directions to be applied to all subsequent drawing operations, we can set up the lM31 and lM32 elements to reflect this as follows: | ||
[[Image:Trans-PM-Fig5.gif]] | [[Image:Trans-PM-Fig5.gif|200px]] | ||
So, with our transform set up to do the translation, assume that you have a coordinate (20,20). Multiplying this coordinate against our transformation matrix, using standard matrix mathematics, the resultant coordinate reflects the translation having taken effect, as follows: | So, with our transform set up to do the translation, assume that you have a coordinate (20,20). Multiplying this coordinate against our transformation matrix, using standard matrix mathematics, the resultant coordinate reflects the translation having taken effect, as follows: | ||
[[Image:Trans-PM-Fig6.gif]] | [[Image:Trans-PM-Fig6.gif|480px]] | ||
This multiplication process could also be written as: | This multiplication process could also be written as: | ||
| Line 64: | Line 65: | ||
==Translating and Sizing a Box== | ==Translating and Sizing a Box== | ||
To translate and scale a box, first define a function <tt>DrawBox</tt> that draws a box in the bottom left-hand corner of the window. This function simply draws a box10 pels by 10 pels starting at coordinate (0,0), of the presentation space associated with the window whose handle is passed in on the call. | |||
<code> | |||
void DrawBox( HWND hwnd ) | |||
{ | |||
HPS hps; | |||
POINTL pointl; | |||
// Get a cached PS for the window | |||
hps = WinGetPS( hwnd ); | |||
pointl.x = pointl.y = 0; | |||
// Set the current position to (0,0) | |||
GpiSetCurrentPosition( hps, &pointl ); | |||
pointl.x = pointl.y = 10; | |||
// Draw a 10 by 10 box from the current position in the current color. | |||
GpiBox( hps, DRO_OUTLINE, &pointl,0,0 ); | |||
// Free the cached PS | |||
WinReleasePS( hps ); | |||
} | |||
</code> | |||
Sample Program 1. Drawing a Box | |||
Sample Program 1. Drawing a Box | |||
Next, modify the function to draw the same 10 by 10 box, but first set up a model transform that will offset the box 100 pels in both the x and y directions and will cause the box to be scaled up (enlarged) by a factor of 10 in both the x and y directions. We will call this modified function <tt>DrawTransformedBox</tt>. Query the current settings of the model transform using the <tt>GpiQueryModelTransformMatrix</tt> function and set its new value using the <tt>GpiSetModelTransformMatrix</tt> function. Also, we still set the current position to (0,0) before we draw the box, and we still only draw a 10 by 10 box. All of the work to move the box and scale it is done because the transformation matrix was multiplied in before the points were actually drawn. | |||
} | <code> | ||
</ | void DrawTransformedBox( HWND hwnd ) | ||
{ | |||
HPS hps; | |||
POINTL pointl; | |||
MATRIXLF m; | |||
// Get a cached PS for the window | |||
hps = WinGetPS( hwnd ); | |||
// Query the current contents of the model transform | |||
GpiQueryModelTransformMatrix( hps, 9L, &m ); | |||
m.lM31 = 100; // Translate the x coordinates | |||
m.lM32 = 100; // Translate the y coordinates | |||
m.fxM11 = MAKEFIXED(10,0); // Scale up the x coordinates | |||
m.fxM22 = MAKEFIXED(10,0); // Scale up the y coordinates | |||
// Replace the model transform with our modified one | |||
GpiSetModelTransformMatrix( hps, 9L, &m, TRANSFORM_REPLACE ); | |||
// Set the current position to (0,0) | |||
pointl.x = pointl.y = 0; | |||
GpiSetCurrentPosition( hps, &pointl ); | |||
// Draw a 10 by 10 box from the current position in the | |||
// current color. | |||
pointl.x = pointl.y = 10; | |||
GpiBox( hps, DRO_OUTLINE, &pointl,0,0 ); | |||
// Free the cached PS | |||
WinReleasePS( hps ); | |||
} | |||
</code> | |||
Sample Program 2. Translating and Scaling a Box | Sample Program 2. Translating and Scaling a Box | ||
This very simple example shows how, in very few lines of code, you can define a transform and dramatically change the appearance of the output. | This very simple example shows how, in very few lines of code, you can define a transform and dramatically change the appearance of the output. | ||
==Helper Functions== | ==Helper Functions== | ||
While it is important to understand the fundamental mechanics of the transformation matrices and the meanings of their individual elements, the GPI provides a set of helper functions to do the work of manipulating and setting up the matrices for various operations. These helper functions are: | While it is important to understand the fundamental mechanics of the transformation matrices and the meanings of their individual elements, the GPI provides a set of helper functions to do the work of manipulating and setting up the matrices for various operations. These helper functions are: | ||
GpiTranslate Used to set up coordinate translations | * GpiTranslate Used to set up coordinate translations | ||
* GpiScale Used to set up a scaling transform | |||
GpiScale Used to set up a scaling transform | * GpiRotate Used to set up a transform to do rotation | ||
GpiRotate Used to set up a transform to do rotation | |||
==Rotating a Box== | ==Rotating a Box== | ||
The function <tt>RotateBox</tt> lets you use the model transform with the <tt>GpiRotate</tt> function to draw a series of boxes rotated through 360 degrees in 10 degree intervals . | |||
The function RotateBox lets you use the model transform with the GpiRotate function to draw a series of boxes rotated through 360 degrees in 10 degree intervals . | <code> | ||
< | void RotateBox( HWND hwnd ) | ||
void RotateBox( HWND hwnd ) | { | ||
{ | HPS hps; | ||
HPS hps; | POINTL pointlBox, pointlStart; | ||
POINTL pointlBox, pointlStart; | MATRIXLF m; | ||
MATRIXLF m; | LONG i; | ||
LONG i; | |||
// Get a cached PS for the window | |||
// Get a cached PS for the window | |||
hps = WinGetPS( hwnd ); | |||
hps = WinGetPS( hwnd ); | |||
// This time let's draw the boxes in blue | |||
// This time let's draw the boxes in blue | |||
GpiSetColor( hps, CLR_BLUE ); | |||
GpiSetColor( hps, CLR_BLUE ); | |||
// For this simple example, we will choose an arbitary position | |||
// For this simple example, we will choose an arbitary position | // as the anchor point for each box of (200,200). This will be | ||
// as the anchor point for each box of (200,200). This will be | // the point about which each box is rotated. A nice | ||
// the point about which each box is rotated. A nice | // alternative, as a small enhancement, would be to make the | ||
// alternative, as a small enhancement, would be to make the | // start position be wherever the mouse is clicked in the | ||
// start position be wherever the mouse is clicked in the | // window. | ||
// window. | |||
pointlStart.x = 200; | |||
pointlStart.x = 200; | pointlStart.y = 200; | ||
pointlStart.y = 200; | |||
// Query the current contents of the model transform | |||
// Query the current contents of the model transform | |||
GpiQueryModelTransformMatrix( hps, 9L, &m ); | |||
GpiQueryModelTransformMatrix( hps, 9L, &m ); | |||
// Setup our box coordinates to be 100 by 100 from wherever | |||
// Setup our box coordinates to be 100 by 100 from wherever | // the start position is. | ||
// the start position is. | |||
pointlBox.y = pointlStart.y + 100; | |||
pointlBox.y = pointlStart.y + 100; | pointlBox.x = pointlStart.x + 100; | ||
pointlBox.x = pointlStart.x + 100; | |||
// Draw a series of boxes, each time around the loop we'll | |||
// Draw a series of boxes, each time around the loop we'll | // rotate through an extra 10 degrees, replacing the transform | ||
// rotate through an extra 10 degrees, replacing the transform | // with our newly calculated one. | ||
// with our newly calculated one. | |||
for ( i=0; i<360; i+=10 ) | |||
for ( i=0; i<360; i+=10 ) | { | ||
{ | GpiRotate( hps | ||
GpiRotate( hps | , &m | ||
, &m | , TRANSFORM_REPLACE | ||
, TRANSFORM_REPLACE | , MAKEFIXED(i,0) | ||
, MAKEFIXED(i,0) | , &pointlStart ); | ||
, &pointlStart ); | |||
GpiSetModelTransformMatrix( hps, 9L, &m, TRANSFORM_REPLACE ); | |||
GpiSetModelTransformMatrix( hps, 9L, &m, TRANSFORM_REPLACE ); | |||
GpiSetCurrentPosition( hps, &pointlStart ); | |||
GpiSetCurrentPosition( hps, &pointlStart ); | |||
// Draw a 100 by 100 box. Note that we issue a normal box | |||
// Draw a 100 by 100 box. Note that we issue a normal box | // drawing request. Blissfully unaware that the transform | ||
// drawing request. Blissfully unaware that the transform | // we setup will cause our box to be rotated. | ||
// we setup will cause our box to be rotated. | |||
GpiBox( hps, DRO_OUTLINE, &pointlBox,0,0 ); | |||
GpiBox( hps, DRO_OUTLINE, &pointlBox,0,0 ); | |||
} | |||
} | |||
// Free the cached PS | |||
// Free the cached PS | |||
WinReleasePS( hps ); | |||
WinReleasePS( hps ); | |||
} | |||
}</ | </code> | ||
Sample Program 3. Rotating a Box | Sample Program 3. Rotating a Box | ||
==Summary== | ==Summary== | ||
This article concentrated on just one of the transforms and explored a few of the ways it can be used. Look for future articles on the other transformations in ''The Developer Connection News''. | |||
The only real way to discover the full power of the GPI transformation matrices is to try using them in your applications. I urge all of you that are interested in getting the most out of the GPI to do just that; experiment for yourselves. Indeed, we would love to publish any great samples you might come up with on future releases of The Developer Connection for OS/2 CD-ROM. | |||
The only real way to discover the full power of the GPI transformation matrices is to try using them in your applications. I urge all of you that are interested in getting the most out of the GPI to do just that; experiment for yourselves . Indeed, we would love to publish any great samples you might come up with on future releases of The Developer Connection for OS/2 CD-ROM. | |||
Kelvin R. Lawrence is an architect working on the design of IBM's Workplace OS Graphical Subsystem. He was the Lead Programmer for the development of the OS/2 2.1 Presentation Manager. Kelvin has been a key member of OS/2 development and support since 1986. | ==About the Author - Kelvin Lawrence== | ||
''Kelvin R. Lawrence'' is an architect working on the design of IBM's Workplace OS Graphical Subsystem. He was the Lead Programmer for the development of the OS/2 2.1 Presentation Manager. Kelvin has been a key member of OS/2 development and support since 1986. | |||
'''Reprint Courtesy of International Business Machines Corporation, © International Business Machines Corporation''' | '''Reprint Courtesy of International Business Machines Corporation, © International Business Machines Corporation''' | ||
[[Category:PM Articles]] | [[Category:PM Articles]] | ||
Revision as of 01:00, 23 March 2016
The OS/2 Graphical Programming Interface (GPI) contains many powerful features that let you construct and manipulate graphical shapes. However, many programmers have avoided using these features in their applications. There is a myth, it seems, that the GPI is hard to program to and hard to learn. In reality, this is not the case. This article shows you how the GPI lets you work with its transformation matrices and describes how to setup simple transformations to change the way picture components or whole pictures are drawn.
This article; however, describes some of the effects you can achieve by using just the model transform.
The Model Transform
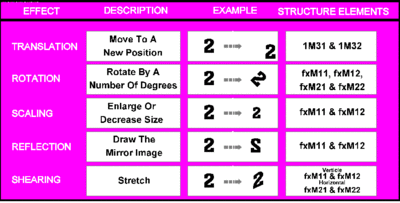
The model transform is a general purpose work-horse transformation that lets you adjust the way a shape is drawn in a number of ways. One or more of the following effects can be achieved:
- Translation: Move the shape to a new position
- Rotation: Rotate the shape by a number of degrees
- Scaling: Make the shape bigger or smaller
- Reflection: Draw the mirror image of a shape
- Shearing: Add a shear to the shape
Figure 1. Different Effects Using the Model Transform
Manipulate each transform by creating and modifying a MATRIXLF structure as defined in the PMGPI.H header file in The Developer's Toolkit for OS/2 2.1.
The MATRIXLF structure is defined in C as:
typedef struct _MATRIXLF { /* matlf */
FIXED fxM11;
FIXED fxM12;
LONG lM13;
FIXED fxM21;
FIXED fxM22;
LONG lM23;
LONG lM31;
LONG lM32;
LONG lM33;
} MATRIXLF;
In more traditional matrix notation, think of the MATRIXLF structure as a three by three matrix as follows:
To get the new value of a point about to be drawn, multiply the (x,y) coordinate against a transform matrix as follows:
As shown in Figure 1, you can combine the different elements of the transformation matrix (MATRIXLF) structure in various ways to achieve various effects:
If you are working with a presentation space created so that the page units are defined as pels, then, by default, the GPI initializes the model transform to identity. In other words, it has no effect on anything. If you multiply an (x,y) coordinate against the transform it remains unchanged. However, if you are working in page units other than pels, the graphics subsystem initializes the model transform to match the page units that the application uses. Given that the GPI uses the lM31 and lM32 elements of the transformation matrix tructure for translating points, the following example illustrates the previous points.
Assuming we are working in pels and that we have not yet adjusted the model transform then it will be initialized as an identity matrix as follows:
Assuming we wanted a translation of 100 pels in both the x and y directions to be applied to all subsequent drawing operations, we can set up the lM31 and lM32 elements to reflect this as follows:
So, with our transform set up to do the translation, assume that you have a coordinate (20,20). Multiplying this coordinate against our transformation matrix, using standard matrix mathematics, the resultant coordinate reflects the translation having taken effect, as follows:
This multiplication process could also be written as:
x' = ( fxM11*x + fxM21*y + lM31 ) y' = ( fxM12*x + fxM22*y + lM32 )
Translating and Sizing a Box
To translate and scale a box, first define a function DrawBox that draws a box in the bottom left-hand corner of the window. This function simply draws a box10 pels by 10 pels starting at coordinate (0,0), of the presentation space associated with the window whose handle is passed in on the call.
void DrawBox( HWND hwnd )
{
HPS hps;
POINTL pointl;
// Get a cached PS for the window
hps = WinGetPS( hwnd );
pointl.x = pointl.y = 0;
// Set the current position to (0,0)
GpiSetCurrentPosition( hps, &pointl );
pointl.x = pointl.y = 10;
// Draw a 10 by 10 box from the current position in the current color.
GpiBox( hps, DRO_OUTLINE, &pointl,0,0 );
// Free the cached PS
WinReleasePS( hps );
}
Sample Program 1. Drawing a Box
Next, modify the function to draw the same 10 by 10 box, but first set up a model transform that will offset the box 100 pels in both the x and y directions and will cause the box to be scaled up (enlarged) by a factor of 10 in both the x and y directions. We will call this modified function DrawTransformedBox. Query the current settings of the model transform using the GpiQueryModelTransformMatrix function and set its new value using the GpiSetModelTransformMatrix function. Also, we still set the current position to (0,0) before we draw the box, and we still only draw a 10 by 10 box. All of the work to move the box and scale it is done because the transformation matrix was multiplied in before the points were actually drawn.
void DrawTransformedBox( HWND hwnd )
{
HPS hps;
POINTL pointl;
MATRIXLF m;
// Get a cached PS for the window
hps = WinGetPS( hwnd );
// Query the current contents of the model transform
GpiQueryModelTransformMatrix( hps, 9L, &m );
m.lM31 = 100; // Translate the x coordinates
m.lM32 = 100; // Translate the y coordinates
m.fxM11 = MAKEFIXED(10,0); // Scale up the x coordinates
m.fxM22 = MAKEFIXED(10,0); // Scale up the y coordinates
// Replace the model transform with our modified one
GpiSetModelTransformMatrix( hps, 9L, &m, TRANSFORM_REPLACE );
// Set the current position to (0,0)
pointl.x = pointl.y = 0;
GpiSetCurrentPosition( hps, &pointl );
// Draw a 10 by 10 box from the current position in the
// current color.
pointl.x = pointl.y = 10;
GpiBox( hps, DRO_OUTLINE, &pointl,0,0 );
// Free the cached PS
WinReleasePS( hps );
}
Sample Program 2. Translating and Scaling a Box
This very simple example shows how, in very few lines of code, you can define a transform and dramatically change the appearance of the output.
Helper Functions
While it is important to understand the fundamental mechanics of the transformation matrices and the meanings of their individual elements, the GPI provides a set of helper functions to do the work of manipulating and setting up the matrices for various operations. These helper functions are:
- GpiTranslate Used to set up coordinate translations
- GpiScale Used to set up a scaling transform
- GpiRotate Used to set up a transform to do rotation
Rotating a Box
The function RotateBox lets you use the model transform with the GpiRotate function to draw a series of boxes rotated through 360 degrees in 10 degree intervals .
void RotateBox( HWND hwnd )
{
HPS hps;
POINTL pointlBox, pointlStart;
MATRIXLF m;
LONG i;
// Get a cached PS for the window
hps = WinGetPS( hwnd );
// This time let's draw the boxes in blue
GpiSetColor( hps, CLR_BLUE );
// For this simple example, we will choose an arbitary position
// as the anchor point for each box of (200,200). This will be
// the point about which each box is rotated. A nice
// alternative, as a small enhancement, would be to make the
// start position be wherever the mouse is clicked in the
// window.
pointlStart.x = 200;
pointlStart.y = 200;
// Query the current contents of the model transform
GpiQueryModelTransformMatrix( hps, 9L, &m );
// Setup our box coordinates to be 100 by 100 from wherever
// the start position is.
pointlBox.y = pointlStart.y + 100;
pointlBox.x = pointlStart.x + 100;
// Draw a series of boxes, each time around the loop we'll
// rotate through an extra 10 degrees, replacing the transform
// with our newly calculated one.
for ( i=0; i<360; i+=10 )
{
GpiRotate( hps
, &m
, TRANSFORM_REPLACE
, MAKEFIXED(i,0)
, &pointlStart );
GpiSetModelTransformMatrix( hps, 9L, &m, TRANSFORM_REPLACE );
GpiSetCurrentPosition( hps, &pointlStart );
// Draw a 100 by 100 box. Note that we issue a normal box
// drawing request. Blissfully unaware that the transform
// we setup will cause our box to be rotated.
GpiBox( hps, DRO_OUTLINE, &pointlBox,0,0 );
}
// Free the cached PS
WinReleasePS( hps );
}
Sample Program 3. Rotating a Box
Summary
This article concentrated on just one of the transforms and explored a few of the ways it can be used. Look for future articles on the other transformations in The Developer Connection News.
The only real way to discover the full power of the GPI transformation matrices is to try using them in your applications. I urge all of you that are interested in getting the most out of the GPI to do just that; experiment for yourselves. Indeed, we would love to publish any great samples you might come up with on future releases of The Developer Connection for OS/2 CD-ROM.
About the Author - Kelvin Lawrence
Kelvin R. Lawrence is an architect working on the design of IBM's Workplace OS Graphical Subsystem. He was the Lead Programmer for the development of the OS/2 2.1 Presentation Manager. Kelvin has been a key member of OS/2 development and support since 1986.
Reprint Courtesy of International Business Machines Corporation, © International Business Machines Corporation