GPIGuide - Coordinate Spaces and Transformations: Difference between revisions
| Line 812: | Line 812: | ||
=== Page-Space to Device-Space Transformations === | === Page-Space to Device-Space Transformations === | ||
There is only one transformation between the page coordinate space and the device space, the device transformation. The device transformation enables applications to work in any presentation-page units regardless of the target device. Unlike the transformations previously described, the device transformation only scales and translates objects, and it is defined by two rectangles. | |||
The | The first rectangle is called the presentation page. Its location is the bottom left origin and its dimensions are fixed. The second is called the page viewport. Its location is the bottom left origin and its dimensions can be varied. | ||
The device transformation, which maps the picture in presentation-page space to device space, happens automatically. The device transformation is established when the presentation space is created, and ensures that graphics are displayed in the correct size and, where possible, that their aspect ratio is preserved. | |||
To modify the device transformation, applications use [[GpiSetPageViewport]]. Input for this function is the device coordinates of the lower-left and upper-right corners of the page viewport. Applications should modify the default device transformation only when it is necessary to use nonstandard page units. | |||
==== Presentation Pages ==== | ==== Presentation Pages ==== | ||
A presentation page is a rectangle in page space | A presentation page is a rectangle in a page space. Its lower-left corner is always positioned at the origin of the page space. | ||
An application can determine the dimensions of the presentation page by calling [[GpiQueryPS]]. It returns a pointer to a SIZEL structure that contains the page dimensions. If an application specifies arbitrary page units when creating a presentation space with [[GpiCreatePS]], the page viewport is constructed such that the origin of the page rectangle maps to the origin of the default device rectangle and either the right or top edge maps to the corresponding edge. Thus, the aspect ratio of the graphic is preserved. | |||
If either the height or width of the presentation page is set to 0 (using [[GpiCreatePS]]), the application must set GPIA_ASSOC to set the default presentation page size to the default device rectangle size. | |||
==== Page Viewports ==== | ==== Page Viewports ==== | ||
Revision as of 17:36, 10 May 2025
Reprint Courtesy of International Business Machines Corporation, © International Business Machines Corporation
A transformation is an operation performed on a graphics object that changes the object in one of four ways: translation, rotation, scaling, and shearing. Transformations enable an application to control the location, orientation, size, and shape of graphics output on any output device.
The transformation of graphics output can be conceptually divided into a series of distinct transformations applied from one logical stopping point to another. Coordinate spaces are used as a method of conceptualizing these logical stopping points. The coordinate spaces are concepts used to explain and manipulate the transformation process.
A graphics primitive in an intermediate coordinate space cannot be displayed on an output device, and a transformation cannot be interrupted at one of the distinct stages. The entire series of transformation steps is applied all at once.
This chapter describes the transformation design process. The following topics are related to the information in this chapter:
- Presentation spaces and device contexts
- Segments and retained graphics
- Clipping
About Coordinate Spaces
Most of the GPI functions draw their output in a conceptual area called the world coordinate space. If you picture the presentation space as a blank canvas on which to draw, the world coordinate space is a Cartesian grid that provides a reference of scale for what is being drawn.
The components of a picture defined in a world coordinate space are often defined to a scale convenient only to that component. Applications also can define each component, or subpicture, starting at the origin (0,0). This enables applications to define the scale of a subpicture and the location of the subpicture separately. The ability to define all subpictures at the origin means there is not always a 1-to-1 correspondence between a presentation space and a world coordinate space. Frequently, a separate world coordinate space exists for every subpicture.
After subpictures are defined in the world coordinate space, they undergo a process called transformation and then appear on an output device. If an application has not specifically applied a transformation to its subpictures, by default, the PM applies the identity transformation, which, in effect, makes no changes to the subpicture.
All graphics systems, not just the PM, use at least one coordinate space to generate output. The simplest graphics systems use a single coordinate space, whose points are the pels on the display. These are sometimes called single-space systems.
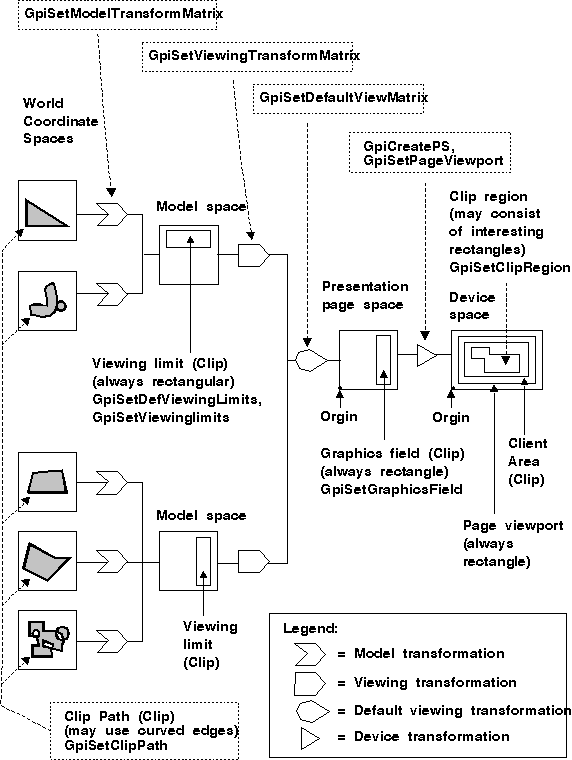
The PM creates multiple coordinate spaces and uses transformations to move subpictures between the coordinate spaces. The PM assembles the application's graphic output in a process that can use up to five coordinate spaces, known collectively as the viewing pipeline. The PM coordinate spaces are:
- World coordinate space
- Model space
- Page space
- Device space
- Media space
For those who are more familiar with a graphics system that uses a single-coordinate space, the following table lists the differences to expect when using PM's multi-coordinate space:
| Single-Coordinate Space Systems | PM Multi-Coordinate System |
|---|---|
| Distances and locations specified in pels. | Seven units of measurement, including pels, are available. |
| Because the shape, or aspect ratio, and size of pels can vary on different devices, the graphic primitives on one device might look different on another. | The output is device-independent. |
| Coordinates entered must already be device coordinates. | Coordinates are made device-compatible through the PM. |
Additionally, a single-space system requires that applications keep track of:
- The scaling between the subpictures. Often this is accomplished by forcing the definition of objects to the scale of the picture, instead of to the scale of the subpicture.
- The scaling between the creation space and output space. Often this is accomplished by forcing the definition of objects to the scale of the paper or window, instead of to the scale of the subpicture.
- All aspects of other transformations.
World Coordinate Space
The world coordinate space is where most drawing coordinates are specified. Each primitive in a world coordinate space is defined using the coordinate positions in the primitive's definition. For example, if an application draws a line from (8,4) to (20,75), the coordinate values (8,4) and (20,75) are world coordinates.
The world coordinate space is specified when the presentation space is created with GpiCreatePS. The PS_FORMAT option supports two sizes of world coordinate spaces: short and long. If the size is short (GPIF_SHORT), the world coordinate space is a rectangular Cartesian space with maximum coordinates of (32767, 32767) and minimum coordinates of (-32768, -32768). If the world coordinate space is short, it is the application's responsibility to ensure that the coordinates defining the subpicture fall within this range.
The second size, long (GPIF_LONG), is the default for the world coordinate space. Most GPI functions that direct their output to the world coordinate space, for example GpiLine, accept 32-bit integers as parameters. A 32-bit integer is equivalent to a rectangular Cartesian space with maximum coordinates of (134217727, 134217727) and minimum coordinates of (-134217728, -134217728).
World coordinates do not have to be within the range of the presentation page. A graphic image that requires a high degree of detail and precision might use most or all of the available coordinate range. A transformation is used to scale the graphic image down to an appropriate size. The actual presentation page size is unimportant in most cases. It is used with the page viewport to redefine the device transform if GpiSetPageViewport is called.
An application can use a clip path clipping area to define the part of the world space to place in the next coordinate space (the model space). A clip path is the only clipping region that can be nonrectangular. Its edges can include arcs, curves, and straight lines. The coordinates that define the dimensions and shape of a clip path are always world coordinates. (Clipping is further described in Clipping and Boundary Determination.)
In a world-coordinate space, there can be several graphic primitives. If, however, an application uses the DM_RETAIN drawing mode to store output in graphic segments, the operating system assigns a new world space to each segment. There is also a world space for the drawings outside of segments.
Model Space
Model space is the conceptual area where the separate components of a picture, defined in world space, are brought together. To assemble one or more primitives from world spaces to model space, the application specifies the transformations to occur. Then the PM applies them to each of the components. Model transformations convert world coordinates to model-space coordinates. For example, an octagon and the word STOP, defined individually in separate world-coordinate spaces, can be assembled into a stop sign in model space.
Graphics applications can have more than one model space. If there is more than one model space, the picture components are assembled in page space. If an application has each model space in a different segment, the model transforms are reset for each segment.
An application can use a viewing limit clipping area to define the part of a model space to place in the next coordinate space (the page space). A viewing limit is always rectangular, and the coordinates that define its location and dimensions are always model coordinates.
Page Space
The page space is where a complete picture is assembled for viewing on a display screen, or for printing or plotting on a piece of paper. Page coordinate units can be increments of an inch, a meter, pels, or some arbitrary value. An application uses GpiCreatePS to specify the units used for page coordinates.
If the application uses retained-drawing mode, the picture in page space contains parts of models (or pictures) from each of the model spaces that have not been clipped. The picture also contains any additional unclipped graphics-primitive output that the application generated in nonretained-drawing mode. If the application uses nonretained-drawing mode, the picture in page space contains all the graphics-primitive output that has not been clipped.
In the page space, an application can use a rectangular clipping area called a graphics field to define the part of the page space to place in the next coordinate space (the device space). The coordinates that define the location and dimensions of the graphics field are always page coordinates.
The page space contains the presentation page whose size and units are defined when creating the presentation space with GpiCreatePS. The presentation page is a rectangle in page space.
Device Space
The device space is the coordinate space in which a picture is drawn before it appears in a display screen window or on the printer or plotter.
Device space is defined in device-specific units. Depending on the page unit used, device-coordinate units can be pels, increments of an inch, increments of a meter, or arbitrary. For example, if the page unit is pels, the device-coordinate unit is pels; if the page units are arbitrary, the device-coordinate units are arbitrary.
Media Space
The media space is used only with windows. When an application draws a primitive at a specified location in a window, it is not actually drawing in the device space, as the device is the entire terminal screen.
Drawing in a window involves a shifting transformation which moves a drawing from the given (unitless) position, to a position in the specified window.
About Transformations
The coordinate spaces are connected by different transformation functions. In reality, the input coordinates of the world coordinate space are transformed directly into device coordinates in a single operation. The intermediate coordinate spaces exist only to provide a useful model to assist in the understanding of how to define the different transformation matrices.
Transformation of graphic primitives occurs when a transformation matrix is applied to those primitives. The individual transformations introduced here do not actually transform the primitives, but rather define portions of the transformation matrix. After all portions of the matrix are identified, the actual operation is performed in a single step.
The transformation functions manipulate graphics primitives as they move from one coordinate space to the next. Transformation functions usually begin with the letters Gpi. Most of the function names have a transformation type that identifies the entities on which it operates. For example, a model transformation is the transformation type that transforms graphics primitives between a world coordinate space and a model space. There is a 1-to-1 correspondence between these transformation types and the actual functions. The transformation matrix data structure is called MATRIXLF.
The following figure lists the sequence of coordinate spaces and the transformation types between the coordinate spaces. Internally, all transformations are combined, and the resulting values are held in the same format as the individual components. By default, there is no viewing window and no graphics field. The application can use the default page viewport. Clipping regions for each coordinate space are also shown.
Identity Transformation
The identity transformation is the default transformation between all coordinate spaces. The identity transformation makes no change to the original coordinates of an object. This transformation is also referred to as the unity transformation, because of the mathematical matrix used to make this transformation.
The identity matrix looks like this:
┌ ┐
│ 1 0 0 │
│ 0 1 0 │
│ 0 0 1 │
└ ┘
(Transformations are accomplished with matrix multiplication; and 1, not 0, is the multiplication identity.)
If a transformation is not explicitly specified, the identity transformation is used to create that portion of the transformation matrix. Most transformations applied to a primitive can be in addition to, or instead of, the current transformation.
Moving through Coordinate Spaces Using the Identity Transformation
The effects of transformation can be minimized by defaulting to the identity transformation. This means that no deliberate action is requested by the application.
Graphic primitives are drawn in their own coordinate scale in world coordinate space. The primitives are then combined in model space. Neither the world coordinate space nor the model space have "real world" units associated with them. This means that if an application draws a line on the x-axis from -300000 to +300000, the line exists as a line 600000 Cartesian units long in both world coordinate and model space.
Page space is the first of the coordinate spaces to be associated with units such as millimeters or inches. These units are set with the GpiCreatePS option PS_UNITS. If the application specifies the option PS_UNITS with the value PU_ARBITRARY, the page space remains unitless; units are applied when the output is drawn in device space.
As an example, assume that the units PU_LOMETRIC (0.1 mm) have been chosen. Again, assuming the identity transformation between model and page space, the primitive appears in the page space as a line that extends:
- 300000 * 0.1mm to the right of the origin
- 300000 * 0.1mm to the left of the origin
A presentation page, a rectangle in page space, has its size defined when a presentation space is created with GpiCreatePS. The presentation page format is defined with the GpiCreatePS option, PS_FORMAT. The three choices for that option are:
- GPIF_DEFAULT - 32-bit integers or 2GB
- GPIF_LONG - 32-bit integers
- GPIF_SHORT - 16-bit integers or 32KB
PS_FORMAT affects the number of units permitted along the coordinate axes of the presentation page. If the choice was GPIF_LONG or GPIF_DEFAULT, and, for example, PS_UNITS remains PU_LOMETRIC, the presentation page axes could range from 0 to 134217727 0.1mm. If the choice was GPIF_SHORT, the coordinate axes could range only from 0 to 32767 0.1mm. These limits are the maximum number of units; presentation pages are usually much smaller.
The presentation page does not affect the primitive in presentation space; it determines what parts of the primitive are visible. With no transformation to scale down the primitive from the model to the page space, the presentation page acts like a sheet of cardboard with a rectangular hole. Only the part of the page space behind the "hole" is visible in page space. The view of everything else is blocked by the "cardboard". Only what is visible in the page space is drawn to the next coordinate space.
Continuing with the example of the 600000 units line above, if GPIF_LONG (or GPIF_DEFAULT) is selected, the 600000 unit line could easily be viewed in the presentation page. If GPIF_SHORT is selected, the maximum presentation page size is 65534 * 0.1 mm units long. In this case, much of the 600000 unit line would not be drawn into the next coordinate space.
The device space is not affected by the PS_FORMAT option. Whether GPIF_LONG or GPIF_SHORT, the device space is a rectangle with maximum coordinates of (32767, 32767) and minimum coordinates of (-32768, -32768). Note that not all of this rectangle is visible, since real devices are not that big. The device space relates to the physical device.
The transformation between the page and device space is handled automatically by the PM. The presentation page is mapped into a rectangle in the device space called the page viewport. This transformation is based on the parameters and options of GpiCreatePS.
Confusion can arise because the effects of the presentation page and the page viewport appear to be a clipping of the primitives in page and device space. While the action taken is identical, the term clipping is reserved for the activity deliberately designated by the application with clipping functions.
Applying Transformations Other Than the Identity Transformation
To better understand the workings of transformations other than the identity transformation, an example of the picture assembly process is illustrated in the following figure, and a detailed explanation follows. 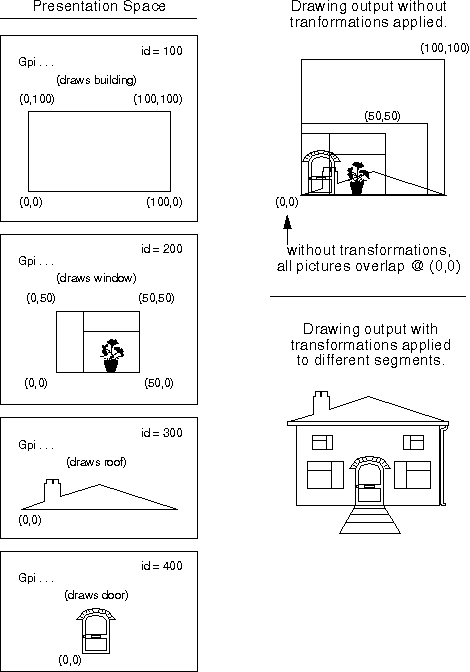
In the world space of the preceding figure, four segments are drawn, each containing a different subpicture. The units of the subpictures can be different (for example, the building might be measured in feet, while the window might be measured in inches), because each subpicture is converted to the scale of the completed picture when it is transformed into the completed picture. All of the subpictures in the previous figure are defined at "real world" scales in their own (Cartesian) world coordinate space.
The difference between applying and not applying transformations can be seen in the model space in the previous figure. Without transformations, the subpictures would be drawn at exactly the coordinates given in the world space, and thus all four subpictures would overlap. With transformations, the subpictures can be scaled and translated to the scale of the final picture. The window subpicture, Segment id=200, has been scaled, rotated, and translated.
The model space contains the model of what the application is trying to draw. There can be more than one model space for very complex drawings, but this is not a recommended style of programming.
The building also resides in the page space and is prepared in the device space for printing on an 8 and a half by 11 sheet of paper. This is shown in the following figure. Most often, the page space to device space transformation (the device transformation) is the identity transformation. 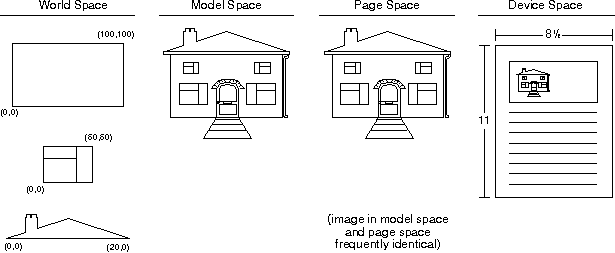
The transformation process in the previous figure is acting on segments. To draw the composite picture in model space, create a segment chain that plays all four segments associated with the building. The purpose of the world-to-model-space transformation is to transform the graphic segments into a composite picture.
Having built the composite picture, the next step is to map the composite into the page space. Usually, the model-to-page-space transformation is the identity transformation. The different coordinate spaces are shown in the previous figure.
The user might want an exploded diagram as well as the composite picture. This is illustrated in the following figure. To create the exploded diagram, the application must draw the segment chain again, with a slight translation down, and scaled up (enlarged) with a very large scaling factor.
Again, while it is possible to create several complex images in different model spaces that must be assembled in the page space, the most frequent use of the page space is to prepare a view of the model-from-model space with the first application of "real world" units such as inches or millimeters. As shown in the previous figures, both world and model space share unitless Cartesian coordinates.
The usual purpose of the page space is to show multiple views of the image residing in the model space, as shown in the following figure. 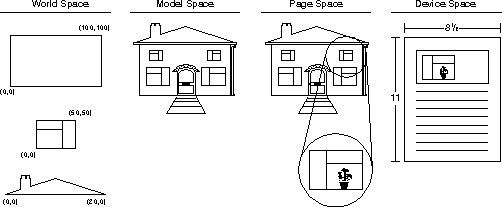
The enlarged image on the right side of the page space is drawn after the image on the left. It therefore has a higher priority and therefore would be drawn on top of the left side image. To obtain a multi-viewed page space image, the application defines a clipping region, and applies this region to the second (enlarged image) playback of the segment chain. The clipping region permits the enlarged image to appear only on the right side of the page space.
The same building also resides in this model space, but it resides in the page space, along with an exploded view of the uppermost right side window. The view is enlarged to such a magnitude that the details of the window are once again evident. If the images in world coordinate space are not able to be drawn in the amount of detail now supported by the PM, then drawing details, such as an exploded view, would reveal the barrenness of the image.
Subpictures can be drawn in world coordinate space without being drawn inside a graphics segment.
Combining Transformations Between a Coordinate Space Pair
There is more than one transformation between the world coordinate and model spaces, and between the model and page spaces. Depending on the desired output, the transformations can be combined in different ways.
World Coordinate to Model Space Transformation Combinations
| Transformation Function | Effect | Transformation Type Sequence |
|---|---|---|
| GpiCallSegmentMatrix | ADD | M I S |
| PREEMPT | I M S | |
| REPLACE | I S | |
| GpiDrawSegment (Call Segment) | Drawing outside of an instance drawing primitive but inside a segment. | M S |
| No specific function | Drawing outside of segments altogether. | M |
Abbreviations: I - Instance Transformation, M - Model Transformation, S - Segment Transformation
Model to Page Space Transformation Combinations
| Transformation Function | Effect | Transformation Type Sequence |
|---|---|---|
| GpiSetPageViewport | Drawing inside of and outside of segments. | V D |
| GpiSetDefaultViewMatrix | Drawing outside of segments. | D |
Abbreviations: V - Viewing Transformation, D - Default Viewing Transformation
Transformation Mathematics
The transformation of a picture can be represented in general terms by two linear equations that define how the (x,y) coordinates of each point in the picture are changed:
┌───────────────────────────────────────────┬─────────────────────────────────────────┐ │ The general form of these equations is: │ where │ │ │ │ │ x' = Ax + Cy + E │ (x,y) defines the original point │ │ │ (x',y') is the transformed point │ │ y' = Bx + Dy + F │ A, B, C, D, E, and F are constants. │ │ │ │ └───────────────────────────────────────────┴─────────────────────────────────────────┘
The transformations that result from these equations depend on the values of the constants, which in turn vary according to the type of transformation being applied.
The operating system handles transformations by using matrix mathematics. In the matrix mathematics:
- Translation is an addition operation
- Scaling, reflecting, rotation, and shear are multiplication operations.
If all the transformations were multiplication operations, different types of transformation could be applied with a single transformation operation. Therefore, to facilitate the combining of calls, translation in the IBM OS/2 is performed as a multiplication operation, rather than an addition operation.
This requires that the vector representing a point, [x y], be extended by a third component, w: [x y w]. This enables all the transformations to be handled in a uniform manner.
This is called a homogeneous coordinate system. The value, w, is a multiplier, so that the point represented is: (wx, wy).
Note: The PM does not support a 3-dimensional presentation space. The 3-dimensional matrix is created to effect matrix multiplication.
In this notation, the point (x, y) is represented as [x y 1]. To be able to operate on such three-element vectors, and to combine translation with the multiplication operations, the 2-by-2 matrix has to be extended to a 3-by-3 matrix, with the third column being:
0
0
1
┌────────────────────────────────┬─────────────────────────────────────────┐
│ The linear equations: │ become the matrix equations: │
│ │ ┌ ┐ │
│ x' = Ax + Cy + E │ │ A B 0 │ │
│ │ [ x' y' 1 ] = [ x y 1 ] * │ C D 0 │ │
│ y' = Bx + Dy + F │ │ E F 1 │ │
│ │ └ ┘ │
└────────────────────────────────┴─────────────────────────────────────────┘
In standard matrix notation, you have:
┌ ┐
│ Msub11 Msub12 Msub13 │
[ x' y' 1 ] = [ x y 1 ] * │ Msub21 Msub22 Msub23 │
│ Msub31 Msub32 Msub33 │
└ ┘
Model for Building the Transformation Matrix
The transformation matrix shown above can be set equal to an entity as complex as:
M*I*S*V*D
where * symbolizes matrix multiplication. As mentioned earlier, all the transformation types might not have a distinct value at all times. One, or all, could simply be the identity transformation.
These intermediate space and step-wise transformations are not actually how the operating system performs transformations. The reason for this relates to the way the PM stores transformation information. The transformation matrix data structure MATRIXLF, undergoes continuous modification during the drawing process, and it can be influenced by more than one transformation function from the application responding, for example, to what a user wants the drawing to look like.
For example, after creating the model of a building from drawing primitives, the user might want to see two identical buildings side-by-side. The application has already applied a series of transformations to the two segments in world coordinate space to create the model of the building. If the application, rather than the PM, had to perform the entire transformation over again from start to finish, it would have to keep track of much more detail. The PM enables applications to process a smaller portion of the MATRIXLF structure, in this example the "V" or "V and D" component, to enable the user to see two buildings side-by-side.
MATRIXLF, the Transformation Matrix
For all the transformation functions, the 3-by-3 transformation matrix is specified as a one-dimensional array in the following order:
(M11, M12, 0, M21, M22, 0, M31, M32, 1)
This one-dimensional array corresponds to the data structure, MATRIXLF. The elements in the data structure correspond to the matrix multiplication constants, as shown in the following table:
| Transformation Type | Matrix Values |
|---|---|
| Scaling, Reflection | M11 and M22 |
| Rotation | M11, M12, M21, M22 |
| Translation | M31 and M32 |
All nine elements do not have to be specified for every transformation function. However, those specified are interpreted as the first n of the nine. If the third, sixth, and ninth elements are specified, they must be 0, 0, and 1 respectively.
MATRIXLF Structure
Of the nine fields in MATRIXLF, four are special 32-bit FIXED variables. The remaining five are 32-bit long integer variables.
The scaling, reflecting, and rotation constants, M11,M12,M21,M22, are the 32-bit, signed, FIXED variables, with an implied binary point between the second and third bytes. The translation constants, M31 and M32, and the three third-column variables, are 32-bit long integers.
A FIXED variable is a binary representation of a floating-point number. A FIXED variable has two parts:
- The high-order 16-bits, which contain a signed integer in the range -32768 through 32767.
- The low-order 16-bits, which contain the numerator of a fraction in the range 0 through 65535.
- The denominator for this fraction is 65536.
For example, to store the cosine of 60° (0.5) in a FIXED variable, an application would multiply 65536 by 0.5. The result, 32768, would be the value to assign to a field in the MATRIXLF structure.
To store a scaling factor of 3 in a FIXED variable, the application would multiply 65536 by 3. Again, the result, 196608, would be the value to assign to a field in the MATRIXLF structure.
MAKEFIXED Macro
The MAKEFIXED macro provides a quick and convenient method for setting the value of FIXED variables. This macro requires two arguments: the first is the integer part of the FIXED value, and the second is the fraction part of the FIXED value. In the following example, MAKEFIXED is used to assign the FIXED value equivalent of 1 1/8 to the matrix component M11.
matlf.fxM11 = MAKEFIXED(1, 8192)
The first argument, 1, is the integer part of the FIXED value. The second argument, 8192, is the result of multiplying 65536 by 1/8.
If it is necessary for an application to scale or rotate an object, the application can avoid most of these mathematics by using the helper functions, GpiRotate and GpiScale. GpiRotate accepts a rotation in degrees and converts this value into the appropriate fields in the MATRIXLF structure. Similarly, GpiScale accepts a scaling factor and fills in the MATRIXLF structure with the appropriate values.
About Transformation Operations
The available transformations are listed in the following table:
Transformations
| Operation | Result |
|---|---|
| Scaling | Shrinks or enlarges the object |
| Reflection | Creates a mirror image of an object with respect to the x- or y-axis |
| Rotation | Rotates the object |
| Translation | Shifts the object with respect to the origin of the coordinate system |
| Shear | Rotates either all the vertical or all the horizontal lines in an object |
These basic operations can be combined. The PM provides special functions to perform scaling, rotation, and translation and also enables applications to specify the transformation matrix directly. Applications can specify values for more than one type of transformation on a single transformation call.
Transformations are used to manipulate graphic objects as they are being moved from one coordinate space to another. These operations are performed by functions called transformation functions. There are also functions that help perform the transformations called helper functions.
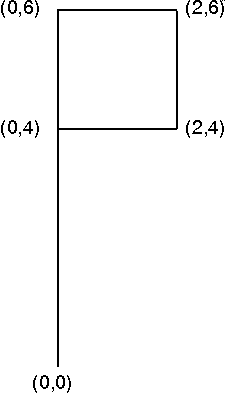
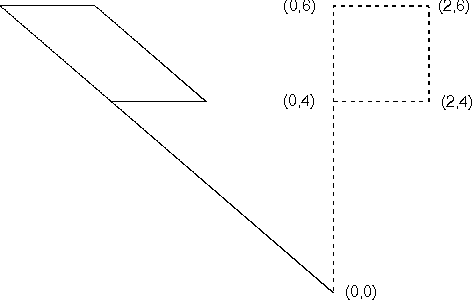
The scaling, reflection, rotation, translation, and shear transformations are best demonstrated by applying them to a picture. The following figure shows the image of a flag before any transformations have been applied. The flag is defined by five points. Their (x,y) coordinates are (0,0), (0,4), (0,6), (2,6), and (2,4).
In the next several sections, where the transformations are described in detail, the effect of the transformation on the flag is illustrated.
Scaling and Reflection Transformations
Applications can scale an object by using GpiScale or by modifying the MATRIXLF structure directly. A scaling transformation reduces or increases the size of a graphics object. A reflecting transformation creates a mirror image of an object with respect to the x- or y-axis.
A scaling factor of:
- greater than 1 causes an increase in size
- greater than 0 but less than 1 causes a reduction in size
- less than 0 causes a reflection about that axis. That is, a negative x scaling factor causes reflection in the x direction.
Note: If an application specifies a scaling factor of greater than 1, the graphics presentation space must be defined with the coordinate format GPIF_LONG. This is because 32-bit matrix elements are required to store these values in retained segment and metafile orders.
The equations to scale by factors Sx and Sy are obtained from the general equations (with M11 = Sx and M22 = Sy) and can be written:
x' = xSx y' = ySy
A scaling transformation reduces or increases all the coordinates of an object by the scaling factor. Any object not aligned on the x- and y-axes is therefore moved nearer to the origin by a reduction in size, and away from the origin by an increase in size. For example, if an application applies a scaling factor of 0.5 to a simple box with its corners at (4,4), (10,4), (10,10), and (4,10), the four corners move to (2,2), (5,2), (5,5), and (2,5).
To scale an object about a point without causing it to move, the following sequence of transformations is required:
- Translate the scaling point of the object to the origin.
- Scale the object at the origin.
- Translate the scaling point of the object back to its original position.
Scaling a Graphics Object
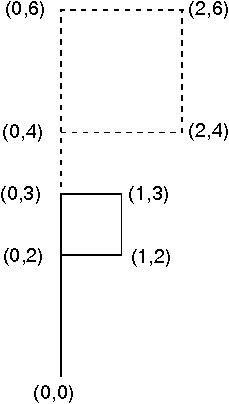
An application can scale the flag by 0.5, by applying:
x' = 0.5x y' = 0.5y
The original five points of the flag are transformed:
- (0,0) → (0,0)
- (0,4) → (0,2)
- (0,6) → (0,3)
- (2,4) → (1,2)
- (2,6) → (1,3)
This scaling preserves the shape and orientation of the object, because the scaling factors in both directions are the same. However, scaling equations permit different scaling factors to be applied to x and y, which can cause distortion of the original shape of the object.
Reflecting a Graphics Object
A negative scaling factor causes a reflection of the object to be drawn. A scaling factor of -1, for example, causes a mirror image of the object to be drawn in the appropriate direction.
MATRIXLF Structure for Scaling and Reflecting
When an application scales an object by using the scaling transformation, the matrix element M11 contains the horizontal scaling component (Sx), and the matrix element M22 contains the vertical scaling component (Sy).
┌ ┐
│ Sx 0 0 │
[ x' y' 1 ] = [ x y 1 ] * │ 0 Sy 0 │
│ 0 0 1 │
└ ┘
If the matrix element M11 contains a negative horizontal reflection component (Sx), it causes reflection about the y-axis. If the matrix element M22 contains a negative vertical reflection component (Sy), it causes reflection about the x-axis.
Rotation Transformations
The application can rotate an object either using GpiRotate or by modifying the MATRIXLF structure directly.
The operating system applies a transformation to all points in the source coordinate space. This means that unless an object is drawn about the origin of the source coordinate space, translation occurs when the object is rotated or scaled. GpiRotate enables an application to specify a point, relative to the origin, that is the center of rotation.
The equations for the rotation of an object about the origin (0,0) through an angle (θ), can be written:
x' = x cos (theta) - y sin (theta) y' = x sin (theta) + y cos (theta)
A negative (θ) value rotates the object clockwise. For clockwise rotation, the rotation equations are:
x' = x cos (theta) + y sin (theta) y' = -x sin (theta) + y cos (theta)
To rotate an object about some other point (p,q), the following sequence of transformations is required:
- Translate the object by (-p,-q) to move the point of rotation to the origin.
- Rotate the object around the origin.
- Translate the object by (p,q) to move it back to its original position.
Rotation preserves the shape and size of the object.
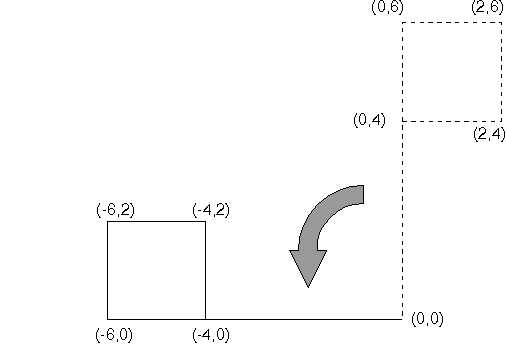
Rotating a Graphics Object
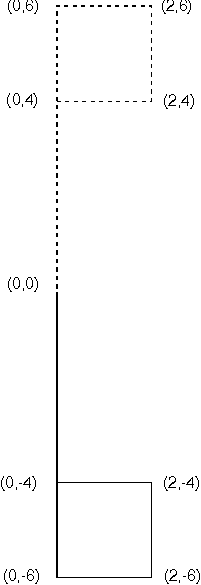
An application can rotate the flag counterclockwise through 90°, by applying:
x' = x cos 90 - y sin 90 y' = x sin 90 + y cos 90
Because cos 90 = 0 and sin 90 = 1, these equations become:
x' = - y y' = x
The original five points are transformed:
- (0,0) → (0,0)
- (0,4) → (-4,0)
- (0,6) → (-6,0)
- (2,4) → (-4,2)
- (2,6) → (-6,2)
MATRIXLF Structure for Rotating
For counterclockwise rotation:
┌ ┐
│ cos (theta) sin (theta) 0 │
[ x' y' 1 ] = [ x y 1 ] * │ -sin (theta) cos (theta) 0 │
│ 0 0 1 │
└ ┘
For clockwise rotation:
┌ ┐
│ cos (theta) -sin (theta) 0 │
[ x' y' 1 ] = [ x y 1 ] * │ sin (theta) cos (theta) 0 │
│ 0 0 1 │
└ ┘
Translation Transformations
The application can translate an object either using GpiTranslate or by modifying the MATRIXLF structure directly.
To move a graphics object by an absolute number of coordinate units, a translation equation is applied. The equations for translation by Tx and Ty are obtained from the general equations (with E = Tx, and F = Ty) and can be written:
x' = x + Tx y' = y + Ty
Translation preserves the shape, size, and orientation of the object. A negative Tx value causes movement to the left. A negative Ty value causes movement downward.
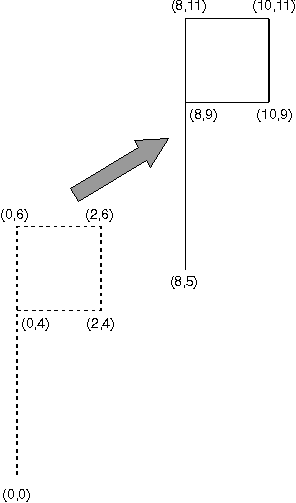
Translating a Graphics Object
If Tx is equal to 8 and Ty is equal to 5, then:
x' = x + 8 y' = y + 5
The original five points are transformed:
- (0,0) → (8,5)
- (0,4) → (8,9)
- (0,6) → (8,11)
- (2,4) → (10,9)
- (2,6) → (10,11)
MATRIXLF Structure for Translating
When an application translates an object by using the translation transformation, the matrix element M31 contains the horizontal translation component, and the matrix element M32 contains the vertical translation component, as follows:
┌ ┐
│ 1 0 0 │
[ x' y' 1 ] = [ x y 1 ] * │ 0 1 0 │
│ Tx Ty 1 │
└ ┘
Shearing Transformations
There are two shear transformations: vertical and horizontal. The vertical shear transformation affects only the y-component of the coordinates of points in an object, and the horizontal shear transformation affects only the x-component.
If an application shears an object that contains two orthogonal vectors (two perpendicular lines), the vectors are no longer orthogonal.
A shearing transformation alters the shape of an object by translating its x-coordinates relative to its y-coordinates, or its y-coordinates relative to its x-coordinates. The amount by which the coordinates are translated is determined by the angle of the shear.
The equation for shearing an object to the left along the x axis by angle (θ) is:
x' = x - y tan (theta) y' = y
To shear an object along the y-axis, the tangent of the angle of the shear is represented by constant B in the general equation.
Shearing a Graphics Object
MATRIXLF Structure for Shearing
For vertical shear transformation, the matrix element M11 contains the horizontal shear component, and the element M21 contains the vertical shear component, as follows:
┌ ┐
│ 1 -tan (theta) 0 │
[ x' y' 1 ] = [ x y 1 ] * │ 0 1 0 │
│ 0 0 1 │
└ ┘
For horizontal shear transformation, the matrix element M21 contains the horizontal shear component, and the matrix element M22 contains the vertical shear component, as follows:
┌ ┐
│ 1 0 0 │
[ x' y' 1 ] = [ x y 1 ] * │ -tan theta 1 0 │
│ 0 0 1 │
└ ┘
About Transformation Functions
Transformation functions manipulate objects between coordinate spaces by applying transformations. Transformation functions require two coordinate spaces: a source coordinate space and a target coordinate space. The choice of transformation function depends on the two coordinate spaces and the desired transformation effect.
The world-to-model space, model-to-page space, and page-to-device space transformations are performed as a single operation. These coordinate spaces are conceptual rather than explicitly defined entities. Describing them separately helps explain the levels of activity during transformations.
All transformation functions share certain parameters, although the values and defaults of those parameters might differ.
Current Transformation
Every graphics object, whether in world, model, page, or device space, has a current transformation value, even if that value is simply the identity transformation.
The default current model transformation is the concatenation of any instance, segment, and model transformations from the root segment downward. The default current viewing transformation is the one most recently specified. The device transformation, set by the page viewport and presentation page, should not be changed while drawing is in progress.
Accumulating Transformations
Each time a transformation function is called, the application can set the function's option parameter to control how the function combines the transformation with existing transformations and the order in which transformations are applied.
| If the application uses this flag... | Then the operating system... |
|---|---|
| TRANSFORM_REPLACE | Replaces any existing transformations with the new transformation. The existing value of the matrix is discarded and replaced by straight substitution. |
| TRANSFORM_PREEMPT | Applies the new transformation before applying the existing transformation. The transformation matrix of the new transformation is pre-multiplied with the transformation matrix of the current transformation. |
| TRANSFORM_ADD | Applies the new transformation after applying the existing transformation. The transformation matrix of the new transformation is post-multiplied with the transformation matrix of the current transformation. |
The order in which transformations are applied affects the appearance of the picture. For example, consider a box primitive with its lower-left corner at (4,2) and upper-right corner at (8,8), scaled by 0.5 and translated by (-10,-10).
If the box is translated before scaling:
The translated box has its lower-left corner at (-6,-8) and upper-right corner at (-2,-2). Each coordinate is then scaled by 0.5, resulting in corners at (-3,-1), (-1,-1), (-3,-4), and (-1,-4).
If the box is scaled before translating:
The scaled box has its lower-left corner at (2,1) and upper-right corner at (4,4). The box is then translated by (-10,-10), resulting in corners at (-8,-6), (-6,-6), (-6,-9), and (-8,-9).
When drawing a picture with called segments and transformations applied to root segments, the root-segment transformations should usually be applied to any segments they call. For example, if a segment translated leftward calls a second segment, that transformation should also apply to the called segment. The application would specify TRANSFORM_ADD in the call to GpiCallSegmentMatrix to add the instance transformation to the calling segment's transformation. Instance transformations are automatically reset on return to the calling segment.
Concatenating Transformations
When applying multiple transformations, an application can concatenate them to produce a final result. To concatenate transformations, multiply the individual transformation matrices. The product is the concatenated transformation.
There are four ways to concatenate the final matrix:
- Hard code the matrix values into the application, then call the transformation functions.
- Multiply the individual matrices, then call the transformation functions.
- Use helper functions with the TRANSFORM_ADD option, then call the transformation functions.
- Alternately apply transformation operations directly to the transformation matrix, then apply a transformation function.
Concatenating before calling provides better performance.
Hard Coding Values for a Concatenated Matrix
Pre-calculating and hard coding concatenated matrix values into the application offers the fastest performance but is rarely practical as transformations are often variable. For example, in interactive graphics with a fixed option like rotating by 90° and enlarging by 4, the matrix values could be hard coded.
Multiplying Matrix Values
Multiplying transformation matrix values directly offers the second-fastest performance and can respond to various transformations. Multiple transformation matrices can be multiplied together. The application is responsible for preventing accumulated transformation side effects.
For example, to rotate an object counterclockwise about point (p,q) using a single transformation call requires three concatenated transformations:
- Translate the object by (-p,-q) to move the rotation point to the origin.
- Rotate the object about the origin.
- Translate the object by (p,q) to move it back to its original position.
The individual matrices are:
┌ ┐ ┌ ┐ ┌ ┐ │ 1 0 0 │ │ cos (theta) sin (theta) 0 │ │ 1 0 0 │ │ 0 1 0 │ │ -sin (theta) cos (theta) 0 │ │ 0 1 0 │ │ -Tx -Ty 1 │ │ 0 0 1 │ │ Tx Ty 1 │ └ ┘ └ ┘ └ ┘
The matrix for the concatenated transformation is produced incrementally. That is, two adjacent matrixes are multiplied to produce a single matrix, which is then multiplied with the third matrix. You can begin by multiplying either the first two matrixes or the second two matrixes. If you start by multiplying matrixes 2 and 3 together, the resulting matrix is:
┌ ┐
│ cos (theta) sin (theta) 0 │
│ -sin (theta) cos (theta) 0 │
│ Tx Ty 1 │
└ ┘
This matrix is multiplied with the first matrix to produce the matrix for rotating an object at the point (p,q):
┌ ┐
│ cos (theta) sin (theta) 0 │
│ -sin (theta) cos (theta) 0 │
│ a b 1 │
└ ┘
where:
a = (-Tx * cos(theta) + Ty * sin(theta) + Tx)
and
b = (-Tx * sin(theta) - Ty * cos(theta) + Ty)
If an application were performing the concatenation for a scaling operation, again it would have to specify the transformation step-by-step. The sequence of actions would be:
- Translate the object's scaling point to the origin.
- Scale the object at the origin.
- Translate the object back to its original position.
Here are the three matrixes required to obtain this effect:
┌ ┐ ┌ ┐ ┌ ┐ │ 1 0 0 │ │ Sx 0 0 │ │ 1 0 0 │ │ 0 1 0 │ │ 0 Sy 0 │ │ 0 1 0 │ │ -Tx -Ty 1 │ │ 0 0 1 │ │ Tx Ty 1 │ └ ┘ └ ┘ └ ┘
The matrix of the concatenated transformation is:
┌ ┐ │ Sx 0 0 │ │ 1 Sy 0 │ │ (-TxSx+Tx) (-TySy+Ty) 1 │ └ ┘
Transformation Helper Functions
Three helper functions are provided to perform the matrix math required to concatenate transformations:
Any of these three functions can be used with the TRANSFORM_ADD option to concatenate the new matrix with an existing matrix. This method builds up the matrix in application storage in a sequence of steps before using a single transform function.
While this is slower than hard coding the matrix, it is faster than alternating between applying transformation operations directly to the matrix then applying a transformation function.
The helper functions merely calculate the appropriate matrix. The transformation is not applied until the array containing the matrix values is passed to the appropriate transformation function.
Applications use GpiTranslate to change the position of an object. The application specifies the coordinates of the point to which to move the object and the name of the transform matrix to use as input to GpiTranslate. The transformation matrix must be in the form of a one-dimensional array. The application also can specify whether this transformation is to replace the value for a previous transformation, or whether it is to be added to it.
Applications use GpiRotate to rotate an object. The application specifies the angle of rotation, the coordinates of the point around which the object is to rotate, and the transformation matrix. The transformation matrix must be in the form of a one-dimensional array. The application also can specify whether this transformation is to replace the value for a previous transformation, or whether it is to be added to it.
To scale an object at a point without also moving the object, applications use GpiScale. When using GpiScale, the application specifies the scaling factor, the coordinates of the center point, and the transformation matrix. The transformation matrix must be in the form of a one-dimensional array. The application also can specify whether this transformation is to replace the value for a previous transformation, or whether it is to be added to it.
An application could alternate between applying transformation operations directly to the transformation matrix, then applying a transformation function with the TRANSFORM_ADD option set. This would build up the matrix in the presentation space. This method has the slowest performance of the concatenation methods.
Round-Off Error
Whenever an application uses transformations, it should handle any round-off error that occurs after multiple scaling, rotation, shear, or reflection transformations. The rounding error increases because a transformation is incrementally updated by the amount of the error with, for example, the TRANSFORM_ADD option. For the rotation to remain accurate, the application should recalculate the transformation, rather than accumulate many small changes.
For example, if an application uses a rotation transformation to rotate the hands of a clock, the accuracy of the clock diminishes due to rounding off after the transformation. The rounding error should be periodically removed by using the TRANSFORM_REPLACE option at known points, for example, every 90° or every complete revolution of the clock.
World-Space to Model-Space Transformations
The model transformation drawing attribute operates between world and model space and can be updated by:
If the model transformation attribute has never been updated, it defaults to the identity transformation. If updated, the existing transformation is the concatenation of instance, segment, or model transformations from the root segment downward. Each time a new segment is opened using GpiOpenSegment, the model transformation attribute resets to its default value.
The three transformations between world and model space are:
- Model transformations
- Segment transformations
- Instance transformations
The transformations that occur between world-coordinate and model spaces depend on the drawing mode and the possible segment type of the drawing primitive.
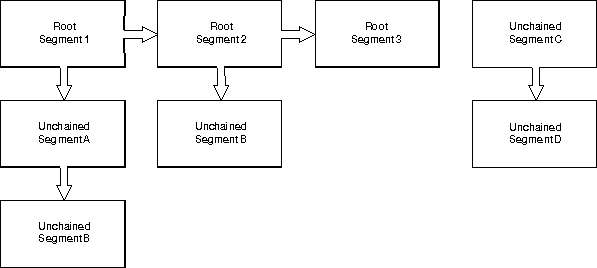
The drawing mode can be either nonretain or retain. Nonretain mode is also called draw mode, as the graphics are immediately displayed. In retain mode, the graphics orders are stored in chained and unchained segments. A series of segments are shown in the following figure.
A model transformation effects objects in any of these segments. A segment transformation affects the six chained segments, on the left and must be issued before Root Segment 1 is accessed. An instance transformation can be applied only to Segment B or Segment D and must be issued from Segment A or Segment 2 or Segment C. The instance transformation is reset on return to the calling segment.
Model Transformations
Model transformations apply to objects inside and outside segments, in retained or nonretained drawing modes, affecting output from:
- GpiDrawChain
- GpiDrawFrom
- GpiDrawSegment
- Any GPI functions outside a retained-drawing segment
Applications can change the model transformation any number of times in a single segment. Changing the model transformation changes the transformation applied to any drawing primitives used subsequently.
An application can determine the values for the current model transformation by calling GpiQueryModelTransformMatrix, model transformation's scaling, rotation, and translation values in a one-dimensional array representing elements in the MATRIXLF structure.
GpiSetModelTransformMatrix specifies the model transformation's scaling, rotation, and translation values applied to subsequent primitives in the segment. As this function does not require the name a segment, it also can be used to apply transformations to primitives outside of segments.
For example, in the building example earlier in the chapter, if the window is stored in a retained segment, an application could draw several identical windows on the house by setting a new translation component in the model transformation before calling GpiBox.
Segment Transformations
The segment transformation provides a way of defining the model transformation drawing attribute at the start of a retained segment. The attribute can subsequently be updated by the model transform orders within the segment. A segment transformation can be applied only to a retained segment.
Segment transformations alter retained-drawing output. Unlike a model transformation, which can be set and reset within a segment bracket, a segment transformation must be set outside of a segment bracket.
An application can determine the values for the current segment transformation by calling GpiQuerySegmentTransformMatrix, which returns the model transformation's scaling, rotation, and translation values in a one-dimensional array representing elements in the MATRIXLF structure.
To apply a segment transformation, applications use GpiSetSegmentTransformMatrix. GpiSetSegmentTransformMatrix can be used to apply any sort of transformation to a segment. For example, it can be used to translate a dynamic segment from one screen position to another, when movement is requested by the user. The application could perform the following steps, for example, on receipt of a WM_MOUSEMOVE message:
- Use the new mouse position to calculate the required displacement from the current position.
- Call GpiRemoveDynamics to remove the dynamic segment from its current position.
- Call GpiSetSegmentTransformMatrix to translate the segment coordinates by the required amount.
- Call GpiDrawDynamics to redraw the segment in its new position.
Instance Transformations
Instance transformations provide a way of defining the model transformation drawing attribute for the duration of a called segment.
Instance transformations alter the retained-drawing output from special segments referred to as called segments. A called segment usually contains a subpicture duplicated several times in other subpictures. The instance transformation positions, sizes, and rotates the subpicture each time the segment is duplicated, because the transformation is set each time the segment is called. An instance transformation applies only to the called segment, and is reset on return to the calling segment. There is no query function associated with the transformation as it must be explicitly set for each called segment.
To apply an instance transformation, applications call GpiCallSegmentMatrix from the calling segment. GpiCallSegmentMatrix calls the segment and also applies the model transformation's scaling, rotation, and translation values in a one-dimensional array representing elements in the MATRIXLF structure and passes a segment identifier.
World Space-to-Model Space Transformation Summary
The following table summarizes the choices available during world-coordinate space to model space transformations.
- World to Model Space Transformation Summary
| Transformation Type | Transformation Function | Applies to... |
|---|---|---|
| Model transformations | GpiSetModelTransformMatrix | Primitives both inside and outside a segment |
| Segment transformations | GpiSetSegmentTransformMatrix | A retained segment, issued at the first element of the segment |
| Instance transformations | GpiCallSegmentMatrix | Only the called segment |
Note: The effect of GpiSetModelTransformMatrix and GpiCallSegmentMatrix on the model transformation attribute can be duplicated by an equivalent drawing order in a drawn retained segment.
Model Space-to-Page Space Transformations
Two transformations operate between model and page space:
- Viewing transformations
- Default viewing transformations
Model transformation types and viewing transformations are part of the picture, while the default viewing transformation is part of the environment and should not be used for picture construction.
Viewing transformations apply in retained or nonretained segments. The viewing transformation attribute is set to the presentation space viewing transformation matrix at the start of each drawn root segment and remains constant for that segment. If GpiSetViewingTransformMatrix is called, the new value applies to the next segment opened. The matrix attribute resets to identity at the segment's end. Each viewing transformation change defines a new model space.
The default viewing transformation is a presentation space attribute and should not be modified mid-picture. It can be updated by GpiSetDefaultViewMatrix. A picture is constructed in the presentation page with an identity default viewing transformation, which can then scale and scroll the entire picture.
A picture is normally constructed in the presentation page with an identity default viewing transformation. The default viewing transformation can then be used to scale and scroll the entire picture in the presentation page.
Viewing Transformations
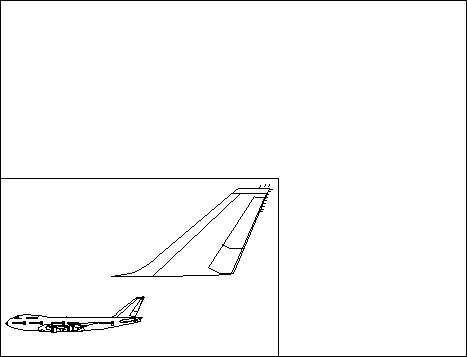
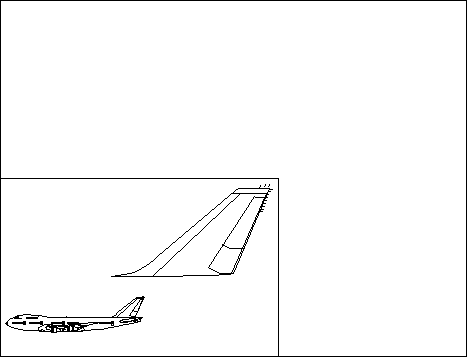
More than one copy of an entire model space can be drawn in page coordinate space, and each copy can be transformed as required. Parts of the model space also can be transformed to the presentation page. For example, an enlarged view of the tail of an aircraft can be shown with a reduced view of the complete aircraft in one corner. This is shown in the following figure.
The entire model space (the aircraft) and a part of the model space (the tail of the aircraft) are drawn to a single page coordinate space. In each instance, scaling and translation transformations have been applied.
Alternatively, the displayed picture can be made up of several subpictures with no common graphical elements. For example, the aircraft can be drawn in one part of the display, and a map of an airport in another part of the display. In this instance, the final picture would be derived from different model spaces.
Whether multiple views are derived from a single model space or from different model spaces, there are two items to address for each instance of a model space incorporated into the presentation page:
- The part of the model space to be displayed must be identified by defining a viewing window for the model space.
- To position and size the contents of the model space in page coordinate space, a viewing transformation must be specified.
To get views of one or more model spaces on the screen simultaneously, each model space is drawn the required number of times. Before each drawing request, the viewing window is defined and a viewing transformation is specified.
Defining the Viewing Window
The viewing window is a conceptual boundary around a part of the model space. To produce the picture in the previous figure, the aircraft is drawn twice. The first time, the viewing window is on only the tail of the aircraft, and the second time, the viewing window is on the entire aircraft. Only those parts of the model space within the viewing window are visible in the picture assembled in presentation-page space. GpiSetViewingLimits is used to define the viewing window.
Graphics Field
Applications also can specify a type of viewing window for the presentation page smaller than the page. This window is known as the graphics field. To define a graphics field, use GpiSetGraphicsField. By default, no graphics field is specified. If a graphics field is defined, the picture assembled within it is the picture that is visible on the output device.
An application can determine the current values for the viewing transformation by calling GpiQueryViewingTransformMatrix, which returns the transformation values in a one-dimensional array representing elements in the MATRIXLF structure. The application can set the values by calling GpiSetViewingTransformMatrix, and passing the transformation values in a one-dimensional array representing elements in MATRIXLF structure.
Default Viewing Transformations
The default viewing window is the same size as the model space. To display entire model spaces, draw the picture the required number of times, letting the viewing window default each time.
Default viewing transformations scroll or zoom pictures in a display window. Query current values using GpiQueryDefaultViewMatrix, returning values in a one-dimensional array representing the MATRIXLF structure. Set values using GpiSetDefaultViewMatrix, passing transformation values in a one-dimensional array representing the MATRIXLF structure.
Default viewing transformations are applied when zooming or scrolling by user interaction. Zooming increases or decreases the size of an area, while scrolling brings off-screen presentation page content into view. The default viewing transformation applies to the entire page coordinate space, added to or replacing the current default viewing transformation after any viewing transformations.
When a presentation page is created, the default viewing transformation is set to identity. To scroll presentation-page contents:
- Erase the screen contents.
- Call GpiSetDefaultViewMatrix to translate the presentation-page picture by the required amount.
- Draw the picture again.
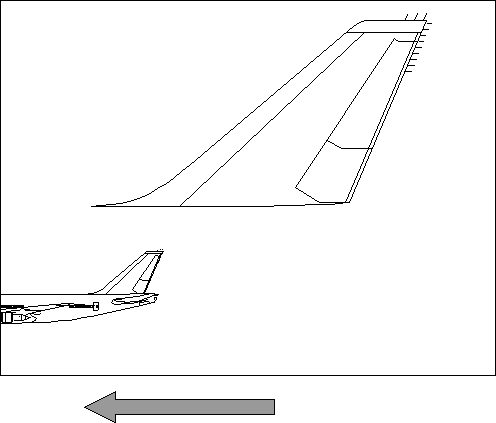
The following figure shows the airplane presentation-page contents scrolled to the left.
- Scrolling the Presentation Page
Every presentation-page coordinate is translated to the left by the same amount.
Zooming is implemented in the same way, except that the default viewing transformation is used to scale the picture up or down as required.
If you want to display only one view of a single picture, and if you do not want scrolling and zooming capabilities, you can let the viewing and default viewing transformations default. When both transformations are permitted to default, page coordinate space is effectively the same as model space.
Page-Space to Device-Space Transformations
There is only one transformation between the page coordinate space and the device space, the device transformation. The device transformation enables applications to work in any presentation-page units regardless of the target device. Unlike the transformations previously described, the device transformation only scales and translates objects, and it is defined by two rectangles.
The first rectangle is called the presentation page. Its location is the bottom left origin and its dimensions are fixed. The second is called the page viewport. Its location is the bottom left origin and its dimensions can be varied.
The device transformation, which maps the picture in presentation-page space to device space, happens automatically. The device transformation is established when the presentation space is created, and ensures that graphics are displayed in the correct size and, where possible, that their aspect ratio is preserved.
To modify the device transformation, applications use GpiSetPageViewport. Input for this function is the device coordinates of the lower-left and upper-right corners of the page viewport. Applications should modify the default device transformation only when it is necessary to use nonstandard page units.
Presentation Pages
A presentation page is a rectangle in a page space. Its lower-left corner is always positioned at the origin of the page space.
An application can determine the dimensions of the presentation page by calling GpiQueryPS. It returns a pointer to a SIZEL structure that contains the page dimensions. If an application specifies arbitrary page units when creating a presentation space with GpiCreatePS, the page viewport is constructed such that the origin of the page rectangle maps to the origin of the default device rectangle and either the right or top edge maps to the corresponding edge. Thus, the aspect ratio of the graphic is preserved.
If either the height or width of the presentation page is set to 0 (using GpiCreatePS), the application must set GPIA_ASSOC to set the default presentation page size to the default device rectangle size.
Page Viewports
A page viewport is a rectangle in device space with variable origin and size. The operating system uses the presentation-page and page-viewport rectangles to define the device transformation.
Query the current page viewport dimensions using GpiQueryPageViewport, returning a pointer to a RECTL structure containing the viewport coordinates. Set the location and dimensions using GpiSetPageViewport, passing a pointer to a RECTL structure with the new values.
The ratio of page width to page-viewport width defines a horizontal scaling factor, and the ratio of page height to viewport height defines a vertical scaling factor. Use DevQueryCaps to obtain the device's horizontal and vertical resolution in pels per meter, typically 0.25 to 0.50 mm.
The page viewport can be shifted in device space by a translation transformation.
Mapping the Presentation Page to the Device
When associating a presentation space with a device context, a default device transformation is set. The page viewport is defined as follows:
| Presentation-page specification | Page viewport size | Usage... |
|---|---|---|
| Pels | The same size as the presentation page | The lower-left corner of the presentation page maps to the lower-left corner of the device space. For example, a presentation page of 300x200 coordinates transforms to a screen area of the same size. |
| Metric units | Coordinates producing the correct matrix for the physical spacing of pels | The lower-left corner of the presentation page maps to the lower-left corner of the device space. |
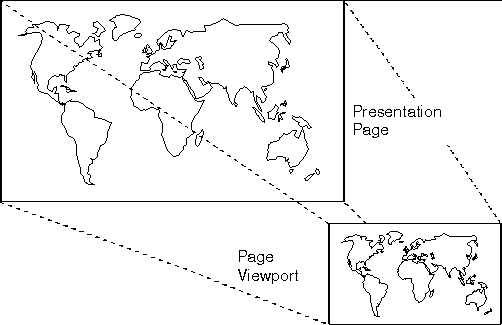
| Arbitrary units | The default size for the device (e.g., maximum paper area for a plotter/printer, maximized window size for a screen) | The page viewport is constructed to give equal x- and y-spacing, mapping the lower-left corner to the device space's lower-left corner, with right or top edges mapped to contain the picture within the device rectangle, preserving its aspect ratio. |
In this example, a world map in arbitrary units, larger than the device space, is scaled to fit the maximized window size, preserving its aspect ratio. The device transformation can be explicitly specified using GpiSetPageViewport.
Coding the Device Transformation
The PM automatically transforms presentation-page contents to the device space area within the page viewport without clipping, as it is a scaling transformation only. The entire picture is displayed regardless of the page viewport size.
A page viewport smaller than the presentation page scales the picture to fit. After transformation to device space, graphics coordinates must be in the range -32768 to +32767, even for GPIF_LONG format presentation pages. Coordinates outside this range cause a coordinate-overflow error. To avoid errors:
- For non-rotated/sheared objects, use GpiConvert to convert device-space limits to world-coordinate-space limits when creating the object.
- For rotated/sheared objects, use GpiConvert to convert device-space limits to model space, ensuring the picture boundary is within these limits, applicable only if all rotation/shearing uses model transformation types.
World-coordinate space limits are:
- -32768 to +32767 for GPIF_SHORT-format presentation pages
- -134217728 to +134217727 for GPIF_LONG-format presentation pages
Although any page viewport size can be specified, the presentation page can only map to an area equal to or less than the available device space. If the viewport is larger, parts of the presentation page are displayed outside the visible device output area. Query the current page viewport dimensions using GpiQueryPageViewport and store them for later restoration.
Device-Transformation Matrix
To manipulate the device-transformation matrix directly, applications need:
- X1: x-coordinate of the page viewport's lower-left corner
- Y1: y-coordinate of the page viewport's lower-left corner
- X2: x-coordinate of the page viewport's upper-right corner
- Y2: y-coordinate of the page viewport's upper-right corner
- XPS: presentation-space width - 1
- YPS: presentation-space height - 1
The device-transformation matrix is: [
[M11, 0, 0], [0, M22, 0], [M31, M32, 1]
] where:
- a = (X2 - X1) / (XPS + 1)
- b = (Y2 - Y1) / (YPS + 1)
- c = X1 + (a - 1) / 2
- d = Y1 + (b - 1) / 2
Windowing-System Transformation
The windowing-system transformation, a translation transformation performed automatically by the PM, maps device-space coordinates to the screen window or printer page coordinates when a picture is first drawn or when the display window is moved.
Transforming Bit-Map Data
Graphics defined in device coordinates (bit maps and image primitives) generally cannot be transformed. For example, an image primitive's size, specified in device coordinates, remains unaltered down the viewing pipeline. However, its position, specified in world coordinates, is subject to translation transformations. GpiWCBitBlt allows the target rectangle to be specified in transformed world coordinates.
Because an image primitive's position is in world coordinates and its width in device coordinates, positioning two images together is challenging. To position a second image, calculate the first image's width in world coordinates:
- Identify two coordinate positions on the image's left and right edges (e.g., (10,80) and (150,80) in device coordinates).
- Convert these to world coordinates using GpiConvert.
- Subtract the lower x-coordinate from the higher x-coordinate to get the width (e.g., the difference between the world-coordinate equivalents of 150 and 10).
With the first image's width in world coordinates, calculate the start position of the second image.
Paths, defined in world coordinates but bound in device coordinates when defined, are device-dependent. Subsequent transformations (except the windowing-system transformation) have no effect on paths. However, if a path creates a wide line, the line's width is scaled as required.
Using Coordinate Spaces and Transformations
This section explains how to:
- Set an application's drawing units to convenient units
- Translate, rotate, and scale a picture
- Shear a picture
Setting Drawing Units
Applications can use GpiCreatePS to set the device transformation to use convenient page units (e.g., centimeters) instead of pels. For a screen output device, open a device context using WinOpenWindowDC. For a printer or plotter, use DevOpenDC. Then create a presentation space using GpiCreatePS, specifying low-metric page units and associating the device context with the presentation space.
Example:
HWND hwnd; /* Client-window handle */
HAB hab; /* Anchor-block handle */
HPS hps; /* Presentation-space handle */
HDC hdc; /* Device-context handle */
SIZEL sizlPage; /* Presentation-page rectangle */
hdc = WinOpenWindowDC(hwnd);
sizlPage.cx = 0;
sizlPage.cy = 0;
hps = GpiCreatePS(hab, /* Anchor-block handle */
hdc, /* Device-context handle */
&sizlPage, /* Address of SIZEL structure */
PU_LOMETRIC /* Centimeters as page units */
| GPIA_ASSOC); /* Associates window DC with PS */
Translating, Rotating, and Scaling a Picture
GpiTranslate, GpiRotate, and GpiScale provide convenient methods for transforming objects in a picture. The following example shows how to translate, rotate, and scale a triangle:
MATRIXLF matlfTransform;
POINTL ptlStart, ptlTrans, ptlRotate, ptlScale;
FIXED fxAngle, afxScale[2];
POINTL aptlTriangle[] = { 575, 300, 575, 500, 500, 300 };
ptlStart.x = 500; /* Starting point x direction */
ptlStart.y = 300; /* Starting point y direction */
GpiMove(hps, &ptlStart);
GpiPolyLine(hps, sizeof(aptlTriangle) / sizeof(POINTL), aptlTriangle);
ptlTrans.x = 75; /* x coordinate for translation */
ptlTrans.y = 75; /* y coordinate for translation */
GpiTranslate(hps, /* Presentation-space handle */
&matlfTransform, /* Address of matrix */
TRANSFORM_REPLACE, /* Replace old matrix with new */
&ptlTrans); /* Coordinates for translation */
GpiSetModelTransformMatrix(hps, /* Presentation-space handle */
9, /* Number of points in matrix */
&matlfTransform, /* Address of matrix */
TRANSFORM_REPLACE); /* Replace old matrix with new */
GpiMove(hps, &ptlStart); /* Move to starting point */
GpiPolyLine(hps, sizeof(aptlTriangle) / sizeof(POINTL), aptlTriangle);
fxAngle = MAKEFIXED(-45, 0); /* Rotate 45 degrees clockwise */
ptlRotate.x = 550; /* x coordinate rotation origin */
ptlRotate.y = 350; /* y coordinate rotation origin */
GpiRotate(hps, /* Presentation-space handle */
&matlfTransform, /* Address of matrix */
TRANSFORM_REPLACE, /* Replace old matrix with new */
fxAngle, /* Rotation angle */
&ptlRotate); /* Origin of rotation */
GpiSetModelTransformMatrix(hps, 9, &matlfTransform, TRANSFORM_REPLACE);
GpiMove(hps, &ptlStart); /* Move to starting point */
GpiPolyLine(hps, sizeof(aptlTriangle) / sizeof(POINTL), aptlTriangle);
ptlScale.x = 550; /* x coordinate scale origin */
ptlScale.y = 350; /* y coordinate scale origin */
afxScale[0] = MAKEFIXED(2, 0); /* Scaling factor on x axis */
afxScale[1] = MAKEFIXED(2, 0); /* Scaling factor on y axis */
GpiScale(hps, /* Presentation-space handle */
&matlfTransform, /* Address of matrix */
TRANSFORM_REPLACE, /* Replace old matrix with new */
&afxScale[0], /* Scaling factor */
&ptlScale); /* Origin of scaling operation */
GpiSetModelTransformMatrix(hps, 9, &matlfTransform, TRANSFORM_REPLACE);
GpiMove(hps, &ptlStart); /* Move to starting point */
GpiPolyLine(hps, sizeof(aptlTriangle) / sizeof(POINTL), aptlTriangle);
Shearing a Picture
The following example shows how to shear a picture by modifying the transformation matrix directly:
MATRIXLF matlfTransform; POINTL ptlStart, ptlEnd; ptlStart.x = 500; /* x coordinate, lower-left corner of box */ ptlStart.y = 300; /* y coordinate, lower-left corner of box */ GpiMove(hps, &ptlStart); ptlEnd.x = 700; /* x coordinate, upper-right corner of box */ ptlEnd.y = 500; /* y coordinate, upper-right corner of box */ GpiBox(hps, DRO_OUTLINE, &ptlEnd, 0, 0); /* Draw first box */ matlfTransform.fxM11 = MAKEFIXED(1, 0); matlfTransform.fxM12 = MAKEFIXED(0, 0); matlfTransform.lM13 = 0; matlfTransform.fxM21 = MAKEFIXED(0, 65536 / 2); /* Shear factor 0.5 */ matlfTransform.fxM22 = MAKEFIXED(1, 0); matlfTransform.lM23 = 0; matlfTransform.lM31 = 200; /* Translate 200 units right */ matlfTransform.lM32 = 0; matlfTransform.lM33 = 1; GpiSetDefaultViewMatrix(hps, 9, &matlfTransform, TRANSFORM_REPLACE); GpiMove(hps, &ptlStart); GpiBox(hps, DRO_OUTLINE, &ptlEnd, 0, 0); /* Draw sheared box */
Using World to Model Space Transformations
The following example shows a sequence of calls applying segment, model, and instance transformations to graphics objects:
GpiSetDrawingMode(DM_RETAIN); /* Sets the current drawing mode to DM_RETAIN */ GpiOpenSegment(segment 1); /* Creates a chained segment */ GpiCloseSegment(); GpiSetSegmentAttrs(); /* Make segment 1 an unchained segment */ GpiOpenSegment(segment 2); /* Creates a retained, chained segment */ GpiSetModelTransformMatrix(TRANSFORM_ADD); /* Specifies a transformation for subsequent primitives, added to the current model transformation */ GpiCallSegmentMatrix(1, TRANSFORM_ADD); /* Calls segment 1 and applies a transformation, added to the current model transformation, applies only to the called segment */ ... GpiSetCurrentArcParams(); GpiPointArc(); /* The 3-point arc is not subject to the transformation specified on GpiCallSegmentMatrix. The prior transformation is applied to the remainder of segment 2 */ GpiCloseSegment(); GpiSetSegmentTransformMatrix(segment 2); /* Specifies a segment transformation for segment 2 */ GpiDrawSegment(); /* Draws segment 2 */
Viewing Transformation
Each time an application draws the model space, it specifies a different viewing transformation to transfer a view to page coordinate space. GpiSetViewingTransformMatrix applies a viewing transformation, with one for each part or whole model space in page-coordinate space.
GpiSetViewingTransformMatrix cannot be called with an open segment and has no effect on primitives outside segments. Once specified, it applies to all subsequent segments until changed and is a fixed part of the segment, unqueryable and unalterable unless the segment is recreated. To solve this for multiple picture versions:
- Define the picture in one or more unchained segments.
- Create a segment chain calling the unchained segments from each root segment.
- Set the viewing transformation before each root segment.
Each segment chain draw produces multiple views of the same picture. Example with a segment chain of three root segments, each calling a single unchained segment:
GpiSetInitialSegmentAttrs(); /* Switches off the chained attribute */ GpiOpenSegment(); /* Creates an unchained segment containing the picture definition */ GpiCloseSegment(); GpiSetInitialSegmentAttrs(); /* Switches on the chained attribute */ GpiSetViewingTransformMatrix(); /* Sets the viewing transformation for segment 1 */ GpiOpenSegment(segment 1); GpiCallSegmentMatrix(); /* Calls the unchained segment */ GpiCloseSegment(); GpiSetViewingTransformMatrix(); /* Sets the viewing transformation for segment 2 */ GpiOpenSegment(segment 2); GpiSetViewingLimits(); /* Specifies the area of interest in the model space */ GpiCallSegmentMatrix(); /* Calls the unchained segment */ GpiCloseSegment(); GpiSetViewingTransformMatrix(); /* Sets the viewing transformation for segment 3 */ GpiOpenSegment(segment 3); GpiCallSegmentMatrix(); /* Calls the unchained segment */ GpiCloseSegment();
The viewing transformation is permanently recorded and cannot be edited without recreating the segment chain, though the picture definition in the unchained segment need not be recreated. If the picture comprises multiple unchained segments, create an intermediate segment for GpiCallSegmentMatrix calls, with each root segment calling the intermediate segment.
The viewing transformation applies to the entire root segment and cannot be overridden within it. It is useful for positioning and scaling subpictures within the presentation page when a segment transformation cannot be used, such as when importing a subpicture using GpiPutData or GpiPlayMetaFile.
Note: The viewing transformation must be set to its default value before defining an unchained segment to be called from another segment.