Into Java - Part XIII: Difference between revisions
mNo edit summary |
|||
| (7 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
{{IntoJava}} | |||
''By [[Simon Grönlund]]'' | |||
{ | |||
[[ | |||
==Into Java, Part 13== | |||
How amazing, this instalment numbers thirteen and the columns now span over three years and two millennia. Now even the puritans can agree on that, December 31th last year the second millennium ended and the third one started. Time is flying away too fast to imagine, but the computer business seems to keep in pace. | |||
This time we will have a discussion on data structures. Fred Brooks once wrote: "Show me your {code} and conceal your <data structures>, and I shall continue to be mystified. Show me your <data structures>, and I won't usually need your {code}; it'll be obvious."--''The Mythical Man-Month, Ch 9''. | |||
Yes, data structures most often is the heart of your implementation, a good choice will reward you several times over, a bad choice and you will regret it over and over again. That is since data structures quickly becomes the skeleton of your application, and as your skeleton hardly is replaced, data structures are hard to replace. | |||
I have said before that good and thoroughly modelling is essential to programming, using papers and a pencil. But how to include the data structures in that planning. This column will entirely discuss that topic. | |||
Mathematics and computer science go hand in hand, so even this time. Hence I will cover a little maths, but do not be scared off, I will not go too deep into that. Further computer hardware works in its own way, and we have to be aware of a few things because of that. | |||
The developers at SUN seems to have read their maths before implementing the Collections framework in Java 2 (see [#note note]), hence we start with a few maths notations, then how these are implemented in data structures. You may also read the interesting pages in the Java API v 1.2 or later, <tt>X/docs/guide/collections/overview.html</tt> there you have to substitute X with your folder, or a URL to SUN's site. | |||
===The math=== | |||
A '''''set''''' is simply described as a collection of elements that need not be ordered. The <tt>Set</tt> interface used in Java follows the hard restrictions that maths states, no two equal elements are allowed. We may think of an alphabet (unordered though), no two equal letters are allowed. On the other hand we are not forced to put every letter we know about in the set, I would hardly put umlaut letters in an alphabet showed to English readers, though I know these letters very well. | |||
< | The Java <tt>Set</tt> is an interface that specifies quite a few methods that a set should have, but Java has a class of the <tt>Set</tt> interface ready to use, the <tt>HashSet</tt>. Further <tt>Set</tt> is implemented by the <tt>SortedSet</tt> interface, that in its turn is implemented by <tt>TreeSet</tt>. (Please do not be worried by the many class names, we will look to some of them, and the remaining ones you may look up in the Java API.) | ||
A '''''list''''' is on the contrary an ordered collection allowing duplicates. Ordered does not imply sorted, only that we know that item "X" is located at index 45, and maybe another "X" at index 201. Or wherever. Only think of a lined up scout patrol, a straight row there everyone has his/her place in the line, though no need to line up by names and two Bill Smith is allowed. | |||
< | Java uses the <tt>List</tt> interface of methods that give us precise control over where we store your objects. We have already used <tt>Vector</tt> that is an implementation of <tt>List</tt>, but there are also <tt>LinkedList</tt> and <tt>ArrayList</tt> to chose from. | ||
Furthermore, '''''map''''' that is more of a function, as sin(60) maps to 0.5, or telephoneNumber(Gronlund, Simon) maps to 1234567, a ''key'' maps to a ''value''. Since a discrete key maps to a discrete value no two duplicate values are allowed. A map is not considered ordered, no straight line of elements is found, nor are they promised to be sorted though some Java classes that follow the <tt>Map</tt> interface are sorted. | |||
<tt>HashMap, Hashtable</tt> and <tt>WeakHashMap</tt> are some classes that implements the <tt>Map</tt> interface, as well as another interface, the <tt>SortedMap</tt> that is implemented by <tt>TreeMap</tt>. | |||
These three fields matches the major interfaces of the Java Collections framework. Java <tt>Collection</tt> also has the <tt>SortedSet</tt>, but we will wait with that until another Java column. | |||
root | root | ||
| | | | ||
| Line 101: | Line 45: | ||
/ \ | / \ | ||
''A binary tree, two branches out of each node'' | |||
Finally, I will mention a very useful structure, namely a '''''tree''''', named so because of its shape. Think of a tree upside down, the root is topmost and the branches grows from the root to the leaves at the end of each branch. | |||
Though many trees used are binary, they have only two branches each node, there are other flavours too. I have used trees with as much as 28 branches each node, but then we are not really discussing ordinary trees and we will leave that for now. Why trees are that popular will be explained in a few minutes but they are, and then binary (and ternary, i.e. 3-branched) trees are the most popular ones. | |||
Trees are a big area of research, included in graph theory, and many interesting results have been found by computer scientists, tailored, used and adopted in the computer industry. Of course trees have found their way into the Java <tt>Collection</tt>, for example <tt>TreeMap</tt>, that is a well thought out piece, and its cousin <tt>TreeSet</tt>, that is something in between. | |||
Before we continue I will introduce a few words, and their meaning. A '''''node''''' is a point in a tree or a list that we may walk to, following a reference. It has at least one reference to it and may have one, two or more references out. Most nodes are made up by a small class, a helper class, that holds the references to 1/ the data, 2/ other nodes whereof one may be the parent node, and 3/ some internal information. Nodes are used on other data structures than trees and works almost the same wherever they are found, as the private and invisible class <tt>Entry</tt> inside <tt>LinkedList</tt> is a node. | |||
< | The non-value <tt>null</tt> is used when there is no reference to another node, and if every variable that should point downwards to another node is <tt>null</tt>, this node is considered a '''''leaf''''', it has data but no legal references. | ||
Accordingly '''''child''''' and '''''parent''''' are used, the child is a node of ''this'' node, and a parent is ''this'' node's superior level node. These terms may be fuzzy when complex structures are used and no obvious levels or ancestors are seen. | |||
The '''''root''''' is often used as the main class of the particular data structure, and holds a reference to the first node but most often no data. The root holds most of the convenient methods that are used on the data structure, such as <tt>add, remove, contains,</tt> etc. Since Java gives us many prefabricated methods we may perhaps be happy with numerous of them. | |||
Finally, the way you need to go from the root to a specific node is called '''''path''''', but in fact any way you need to go in a graph such as a tree is called a path. | |||
===Computer basics=== | |||
From the very beginning technicians have been storing data as '''''bit''''' by bit, normally thought of as 1 and 0, and implemented as distinct electrical values, such as +85mV and -85mV or alike. The bits are held together as a '''''byte''''', now a byte is thought of as an eight bit byte. Do not confuse a byte with the 32 bit (or 64 bit) compound that is called a '''''word'''''. A word is set up by several eight bit bytes. | |||
{|class="wikitable" align="Right" | |||
|- | |||
!Type | |||
!Size | |||
{| | !Range (approximately) | ||
|- | |- | ||
| | !colspan="3"|''Floating-point numbers'' | ||
| | |- | ||
| | | valign="Top" | double | ||
| | | valign="Top" | 8 bytes | ||
| | | valign="Top" | 1.7977E+308, 15 significant digits | ||
|- | |- | ||
| | | float | ||
| | | 4 bytes | ||
| | | 3.4028E+38, 6 significant digits | ||
|- | |- | ||
!colspan="3" |''Integer numbers'' | |||
|- | |- | ||
| | | long | ||
| | | 8 bytes | ||
| | | 9,223,372,000,000,000,000L | ||
|- | |- | ||
| | | int | ||
| | | 4 bytes | ||
| | | 2,147,483,000 | ||
|- | |- | ||
| | | short | ||
| | | 2 bytes | ||
| | | 32,768 to 32,767 | ||
|- | |- | ||
| | | byte | ||
| | | 1 byte | ||
| | | -128 to 127 | ||
|} | |} | ||
In one of the first parts of this Java programming series we looked at the basic data types, let us remind ourselves. First we can see that Java is already prepared for easy handling by 64 bit CPU's, as <tt>double</tt> and <tt>long</tt> is 8 x 8 = 64 bits long. But the smallest compound, the <tt>byte</tt>, is one eight bit byte only. | |||
Shall we now think of how data is stored in the computers working memory (RAM). That is not hard to explain, whenever the CPU reads an instruction that tells it to store a variable (let us say an int) it needs two parts, the data and the address in the memory. The latter is made up by the compiler (and the JVM when using Java) in conjunction with the operating system (OS), and the very smallest area to address is an 8 bit byte. | |||
When the CPU executes that instruction it accesses the RAM at the told address and stores the data there. Another variable may later be stored, and is then stored at another address. The more variables stored the more addresses are used, but there are no distinct rule where these addresses may be located. Hence they may be scattered around, or accidentally be grouped together. But no one variable knows the location of the others, they are no part of a data structure. | |||
===Arrays--the simplest structure=== | |||
A long time ago the array was found as a good way to collect related variables together. We may for example measure the temperature each hour and need a way to store these values, then a 24-element array is suitable, one array each day. | |||
[[Image:java13a.gif|thumb|int array]]An array is simply several variables in a row, the compiler fixed some kind of code that orders a line of consecutive variables as seen in the image and the OS manages that. The advantage from this is that now we only need one address that points to the beginning of the array, held by the reference. | |||
[[Image:java13b.gif|thumb|Object array]]The elements is found as the result from add up the reference with the offset, the first element having zero offset. Here is the reason why arrays, <tt> Vector </tt> and other data structures start at number zero, the offset is zero at the first element. Hence we now can get to "99" by adding 3 to the reference, as <tt> int answer = myIntArray[3]</tt> where myIntArray holds the reference. | |||
Arrays may be used not only with basic data types as <tt> byte, short, int, long, float </tt> or <tt> double</tt>, yes, in fact, with <tt> boolean </tt> as well. But we can add any kind of objects to them; <tt> MyClass[], Integer[] </tt> or <tt> Object[] </tt> are legal, as any class is. If different kind of objects have to be stored in the same array, then use the cosmic <tt> Object </tt> class as the type. | |||
Normal array operations are as follows. Please note that arrays have a convenience variable named <tt> length </tt> that is read directly and not through a method. Also note that arrays always are accessed with square brackets; [ ]. | |||
byte[] byteArray; // declaration only | |||
// later, initiation with size 9 | // later, initiation with size 9 | ||
| Line 235: | Line 171: | ||
String newStr = (String)objArray[0]; // cast is needed | String newStr = (String)objArray[0]; // cast is needed | ||
Integer newInt = (Integer)objArray[1]; | Integer newInt = (Integer)objArray[1]; | ||
... | ... | ||
Using arrays is convenient, and as they are very close to the computer hardware environment they are efficient and do not cause that much overhead. Why not only using arrays then? | |||
< | The first limitation is the length of an array. The length can not be changed dynamically, and that is true for every kind of computer and OS, always. If any programming language looks like having such a feature, that is a fake, beneath the surface there is some kind of functionality fooling us around. That is clearly understood when considering how an array is laid out, the OS gets an order for, let us say, an <tt>int</tt> sized array with 10 elements. That is 10 by 4 bytes (an <tt>int</tt> needs 32 bits and 4 bytes * 8 bits = 32 bits) resulting in 40 bytes in a row. Maybe next step for the OS is an order for one <tt>long</tt> sized variable (8 bytes) and by an unlucky coincidence it is placed at the very next free address after the array. Thus the array can not grow into that spot. | ||
Growing an array is a simple matter of ordering a new one, that much longer as we like it to be. The OS will give us a new and empty one and we then do a simple copy and paste from the original to the latter one using <tt>arrayCopy</tt> of the <tt>System</tt> class. Finally we simply leave the original to destruction and soon the OS will recycle the address area. Exactly the same operation is performed upon shrinking the length. These operations are of course time consuming and considered inefficient. Still many Java classes are based on simple arrays, as <tt>Vector</tt> uses an <tt>Object</tt> array and performs the operations just explained when necessary. | |||
[[Image:java13c.gif|thumb|add]]Else, normal actions on simple arrays are performed efficiently and with no hassle. They are easily understood and not hard to implement. Since Java hides the hazards with pointers and pointer arithmetic the work is a breeze, as the <tt>add</tt> method show us in the left hand image. We simply keeps track of the last index used and add the next element to the next index. | |||
The next inconvenience occurs when we implement the <tt>remove</tt> and <tt>insert</tt> methods, let us discuss them to some extent. The simple <tt>removeLast</tt> and <tt>insertLast</tt> are disregarded as they are implemented as decrementing the <tt>size</tt> variable and <tt>add</tt> respectively. | |||
[[Image:java13d.gif|thumb|remove and insert]]Consider the left part of the image, we remove the second element. Remove is clearly different from assigning the second box another object, remove will leave an empty box, and empty boxes, how would you like to keep track of them? You don't, you have to move every element to the right of the empty box one step leftward. Again that is time consuming, more time is spent the more leftward the removed element was located and the longer the array is. | |||
Exactly the same argument is valid with insert, we have to move every element to the right one step rightward, finally we can add the new element in the obtained empty box. Both methods have the '''''worst case''''' scenario of T( ''n'' ) where ''n'' is the number of elements in the array and T is the time spent on each iteration (computer scientists use the term big-O, but we will leave that). The '''''best case''''' is T( 1 ) since that is simply <tt>removeLast</tt> or <tt>insertLast</tt> discussed earlier. The '''''average case''''' is T( ''n'' /2 ) since the average case is the middle element being changed. To that we most of the times have to add the time to find which index the element we will remove has, or the one to insert is to be given, which doubles the time. | |||
Hence arrays and classes that are built on arrays are good for simple data structures without too many remove or insert. Order an array of the expected length from the very beginning, thus avoiding too many <tt>arrayCopy</tt> operations. Many delicate implementations are built on simple arrays. On the other hand many applications suffer from being built on arrays that do not scale well or suffer from time consuming operations. | |||
===Linked lists--the solution to insert and remove cons=== | |||
[[Image:java13e.gif|thumb|Linked list, insert/remove on a list]] | |||
As the problem with insert and remove came from the time spent on <tt>arrayCopy</tt>, shuffling elements left- or rightward, we would like a data structure that do not need these operations. A linked list is the answer. Think of nodes linked, or chained, together as the uppermost image part shows. | |||
The root knows at least the first node, many times it also knows the last node. If the list is single linked only the <tt>next</tt> reference is used and we can only traverse the list in one direction, going forward. If the <tt>previous</tt> reference is used we have a double linked list and can traverse it both ahead and back, as the image shows. The Java <tt> LinkedList</tt> is a double linked list, also knowing its last node, but note that it is the base class that knows the start and end of the chain, the nodes themselves know only the <tt>next</tt> and <tt>previous</tt>, as well as their <tt>data</tt>. | |||
Now look at the lower part of the image, an <tt>insert</tt> (or is it a <tt>remove</tt>?) is to be done. The methods need to change the <tt>next</tt> and <tt>previous</tt> references to include (or exclude) the "C" node, that is all. Okay then, that is a little tricky but it is nothing more than switching references so that the "C" node's <tt>next</tt> will refer to the same as the "B" node does, then changing the <tt>next</tt> of "B" to refer to the "C" node (note that we talk about the nodes and not the data, but use the data as a label in our discussion). Likewise we set the <tt>previous</tt> of the "C" node to reflect the "D" nodes reference, and then changes the <tt>previous</tt> of the "D" node to refer to "C". The remove is analogous to this procedure. | |||
Hey presto, now both insert and remove will only take T( 1 ) since there is no shuffling elements around. The different objects may be stored anywhere in the computers RAM, still the variables refer to the correct objects. But are there no drawbacks? | |||
Of course there are some drawbacks and some shortcomings, every data structure suffers from limitations and you are the one to chose the best compromise. Handling arrays are efficient in many ways, the data is stored tight to each other and hence derive advantage from the "read-ahead" that most OS's use, from the cache mechanism and a few more benefits. Instantiating objects eats time, we never know were they actually are stored (we do not need to, but the tight data storage is lost) and there is some overhead with objects. | |||
Anyway, quite a few times we decide that we can live with these shortcomings, the usefulness outweighs the shortcomings. But still the worst thing is that methods like <tt>contains(Object)</tt> or <tt>remove(Object)</tt> still have the same best, average and worst cases. How come? Since these methods have to iterate each node until the correct data is found. There is no shortcut to find the correct one, each one has to be examined with a fail or pass. | |||
The same arguments hold if we like to maintain a sorted list (Java LinkedList do not support sortability, but we are free to implement such a list). To sort a "Y" after "X" we have to find "X", and that takes T( ''n'' /2 ) on average. | |||
< | Lists are mainly used to hold queues, methods like <tt>addFirst</tt> and <tt>removeFirst</tt> performs well and the overhead is ignorable in these cases. Unordered collections perform well, except from searching them. | ||
Now we have tracked down to "how to sort into a sorted data structure?" So far we have found no good data structure to maintain a sorted collection and perform operations on that collections efficiently, though the linked list is much better than an array. Any kind of array or list suffers from being linear, it is traversed ahead or backwards. May the tree structure be the solution? | |||
===The binary tree=== | |||
Straight to the point, the tree is outstandingly fast with <tt>insert, remove, contains(Object)</tt> and whatever we like to process on it. Trees belong under ''set'' discussed as the first of three math definitions, a set do not allow duplicate objects stored. | |||
If we consider a huge telephone database, there is not <u>two</u> objects referring to the one individual. If so, the database will soon get unstable and when we update one record the other one will still be reflecting old data. Fulfilling these requirements of no duplicates we can start with instantiating <tt>MyTree</tt>, that is we get ourselves a root to the still not yet created first node. | |||
We pick the first individual and instantiate an object from the data read. Then we pass the data to <tt>add(Object)</tt> that creates a new node referring to the object. Since it is the first node added to the tree it simply becomes the first node the root refers to, and the node itself have only two <tt>null</tt>-references as the <tt>left</tt> and <tt>right</tt> variables. The value of the data is so far irrelevant. | |||
Next individual is instantiated and the object is passed to <tt>add(Object)</tt> that creates a new node. But since it is not the first node added to the tree we have to find out if it is to be placed to the left or the right from the existing node, using the <tt>left</tt> or <tt>right</tt> child of the first node. To make that comparison our object '''must''' be able to answer a compare-to question, that is, we have to have a method named <tt>compareTo</tt>. That method is outlined in the <tt>Comparable</tt> interface that we '''have to''' implement in our class if we are using any of the Java Collections' classes that support sorted collections. | |||
===compareTo(Object)=== | |||
A class implementing the <tt>Comparable</tt> interface only has to implement the single <tt>compareTo(Object)</tt> method. Think of us standing in an object, the <tt>this</tt> object. We receive another object, named <tt>other</tt>, and we have to answer to the question "is the other object lesser than, equal to, or bigger than your object is?" Look at the limited code below. | |||
public class MyShoes '''implements Comparable''' { | |||
short shoeSize; | short shoeSize; | ||
| Line 307: | Line 232: | ||
} | } | ||
} | } | ||
<font size="-1">Naturally other things may guide the comparison of shoes than only the size, but the lesson is the same. We return a negative int value if we are less than the other object, zero if we are equally sized, or a positive int if we are bigger than the other. For example, the <tt> String </tt> class performs a true lexicographically comparison, taking upper and lower cases into account. How we compare objects is up to us, but the comparison has to be done if we like to maintain a sorted collection. | |||
<font size="-1"> | |||
Continuing with the adding to the tree we chose <tt>left</tt> or <tt>right</tt>, less than to the left, else to the right (equal to is not allowed). This time we imagine we got the left choice. Reading the third individual results in the next node, which data shall be compared with the first node's data, left or right. If it is to the left we continue with comparing the new node with the left node's data, the second node made. That is, we have to go one step deeper to make another comparison. Else we can simply add the new node as the right child to the first node. I will try to illustrate it. | |||
I. root II. root III. root IV. root V. root | |||
| | | | | | | | | | | | ||
"Mike" "Mike" "Mike" "Mike" "Mike" | "Mike" "Mike" "Mike" "Mike" "Mike" | ||
| Line 328: | Line 242: | ||
/ / \ / \ | / / \ / \ | ||
"Chris" "Chris" "Len" "Chris" "Len" | "Chris" "Chris" "Len" "Chris" "Len" | ||
For example "Chris" is first compared to "Mike", then to "John" and is then set as the left child of "John", but "Len" is lesser than "Mike" but greater than "John" and was set to the right of "John". But this tree does not look sorted at first sight, does it? Reading a tree in order we first have to find the leftmost node, in our case "Chris" that also is the first name of this collection. From that node one step up to the parent and reading that node, "John", which is correct. Then down the right child one level, and try to find the leftmost node again (which can be a few levels down actually). This time there is no leftmost node of that child so we read the node, "Len", again correct. Try to go down to the right, but there is no right child. Upwards, but we have read John so we leave him and head for his parent, "Mike", that is correct. Does "Mike" has a right child? And does that child has a leftmost node downwards? "Mike" has a child, "Simon", which has no children. We are done. | |||
The rules seems to be, | |||
# try to go left | |||
## if possible, go there and continue from 1 | |||
## else, continue with 2 | |||
# read this one | |||
# try to go right | |||
## if possible, go there and continue from 1 | |||
## else, do nothing, we will recursively return to your parent | |||
and we will get the elements in a sorted way. The recursion is the tricky part to follow, but remember that the computer remembers were it left off for the child, and the parent will continue executing the code were it left off for a while. Since there are such advanced and good Java classes prefabricated I will not give any code here, only links to the recursion instalments, [[Into Java - Part V|Part V]] and [[Into Java - Part VI|Part VI]] that explains the mechanism used. | |||
Now, why use such non trivial structures as trees? Since they give an outstanding performance hit on sorted collections, any kind of look-this-up operation is done fast and quickly, if the object is in the tree it is found that snappily, or it says "the object is not found". Insert-this is executed as quickly. How come? | |||
Here a little more maths is needed. The example above is not that big, but still it shows that each level double the number of nodes, the zero level is only one node, the first level is two of them, "John" and "Simon". The second level is already having place for four nodes, though only two is used. The next level will have eight, the next sixteen and so forth. Clearly we see ''n'' = 2<sup>''h''</sup> where ''n'' is the number of nodes possible, and ''h'' is the height of the tree, the number of levels used, having the first node at level zero. But that is not the whole truth, since each node at each level also may be used and that gives a much better sum of nodes, an expression that reads ''n'' = 2<sup>(''h''+1)</sup> - 1. | |||
Such expressions grow rapidly, only ten levels, including the zero level, will give room for 1,023 nodes, and 20 such levels will gladly accept more than one million objects. Hence I can promise that a telephone number database with one million individuals will never suffer from more than T(20), or more precisely put, the worst case will be T(''h''), where ''h'' may be computed by ''h'' = lg(''n''). But this is not completely true, since that is based on the assumption that all trees grow balanced and equally, which is not a fact. Still the Java classes that support sorted trees are that close to the lg(''n'') that we can forget about the difference. | |||
There is simply no other data structure giving us this splendid performance with that little implementation effort, we can find any person of that one million person telephone database within 20 comparisons, remove him or simply read the data. An insert is made equally fast. Is there any drawbacks then? | |||
Yes, of course there are drawbacks, didn't I told you? <grin> So far we assumed that the input to the tree was picking individuals randomly, but consider moving from one ordered and sorted data structure, that have served for a while, to a tree. We pick the first individual, "Aaron", then comes "Abel", "Abdul", and so forth. "Aaron" will of course be the first and topmost node, but "Abel" will surely be bigger than him and set as the right child. So will "Abdul", "Abraham" and every other individual be, set as the right child to the right child, no one will ever be placed to the left. The result is again a linked list and the last person will be that many levels away from the root. | |||
Apparently a tree is not suited for that kind of input, but else it works nice. There are naturally several ways to solve the dilemma, pick the objects at random and watch out for picking the same twice and not to forget someone, or start at the middle and then recursively pick the elements as in the recursions discussed in [[Into Java - Part VI|instalment 6]]. Or any other method of your mind. | |||
To avoid heavy unbalance in trees something named the red-black tree was invented and implemented, in fact it is used by Java <tt>TreeMap</tt>. It promises that no path is more than twice as long as any other path, thus giving us a reasonable balanced tree. Consider that the more precise balancing we require the more overhead it causes the tree's balancing mechanism. And there is not much difference between 10 and 20 levels, not compared to the up to one million look-ups on a list or array, or 500,000 on average. | |||
===The map, hash and table=== | |||
[[Image:java13g.gif|thumb]][[Image:java13f.gif|thumb]]Still the data structures we have examined do not have T(1) at look-ups. Is there a way to get such good results? Yes, the mapping concept gives that performance. Consider having an array with 30 empty indexes, and a function that takes the object, or a key, and computes something (a pseudo-index) that can be mapped to an index of were to put the object. If that function promises to always compute the same pseudo-index from equal keys, and also to spread these pseudo-indexes equally along over a fix length, then any look-up or insert will execute with T(1). This data structure is mainly called hash table or hash map since we '''''hash''''' the pseudo-index, called the hash value, from the key. That hash value is mapped into an index of the array and the object is put in a table or a map. Are there any drawbacks <grin>? | |||
Collisions, when it happens that two unequal keys gives the same index (rare but possible), cause a drawback that gives us some headache, we have to take care of the situation and that will increase the time consumed somewhat. Another drawback is the same as with arrays, if the table grows to much we have to lengthen the array. But we cannot use the speedy <tt>arrayCopy</tt>, instead we have to re-hash (re-map the hash values) of every object since now we have more indexes to chose from and the look-up function will map the hash value onto that many indexes, not onto the previous length. This re-hashing wastes a lot of time, but can be prepared for by giving the table a good initial size. | |||
Also, to avoid too many collisions we must waste some memory, some unused memory. The benefit is that the mapping will be wider or broader and thus the chance is better that a collision will not occur. It is not correct, but simple, to say that there are more free slots to pick from. Incorrect since the mapping does not use the free/not-free state in its calculation of the index. But it is simple since the more free slots there are the better chance to get a free one. Normally a hash table uses a ''load factor'' of 0.75, it wastes at least 25% memory space, "a good trade-off between time and space costs" as the Java API states. | |||
Finally the default hash table does not allow duplicate objects, that is since the hash function will produce the very same hash value again and if there is no way to tell two identical objects apart, how will the computer do then? Adding two "John Smith" objects will not be good, but maybe there are two such persons but they have different addresses, birth date etc., that can be used by the hash function too. | |||
Or, better, we '''have to''' follow the rule that says that we should have an <tt>equals(Object)</tt> method in your added object. That is, we have to implement a method that can tell apart different objects, even though they look alike, and return a boolean <tt> true</tt> or <tt>false</tt>. There is an <tt>equals(Object)</tt> in the <tt>Object</tt> class, but that can only tell apart objects that are truly stored at different locations of your RAM, it does not compare them on a more solid basis. Hence, if we by mistake make two objects based on the same person, or whatever, they are considered not-equal by that method, though they in real life are one. | |||
====put and get==== | |||
Since mapping structures have that nice performance they are used quite often. But the way to use them differs from the previous structures that used a simple <tt>add(Object)</tt> method. First we have to implement the two methods mentioned, <tt>hashCode</tt> and <tt>equals</tt>, both described in the <tt>Object</tt> class. (Sometimes the methods of <tt>Object</tt> is sufficient, then we are done.) | |||
< | Unfortunately the description on <tt>hashCode</tt> does not tell the range of the int to return. Do not worry, any valid integer is okay. The hard thing with hashCode is to find out how to equitable spread out the result. The best case is when two distinct objects, differing only by a fraction, are not given hash values close to each other (guess if there is much toil spent on finding good hash functions). Given the hash value the table will compute it into an appropriate index based on the tables actual size and the load factor wished, and finally add the object somewhere in the array. | ||
< | The <tt>equals(Object)</tt> method is still the heart of the hash table functionality. It is up to us to decide the basis for equality. If we are sure that no two objects will be instantiated from the same source (e.g. a person), we can rely on the <tt>Object</tt> class. Else we have to think about how to tell objects apart, and return a <tt>true</tt> or <tt>false</tt>. | ||
Next step is described in the code below. Notice that '''we''' do not make any use of the <tt>hashCode</tt> or <tt>equals</tt> methods, but the table does. Since the Java <tt>Hashtable</tt> follows the Map interface we use the two methods <tt>put</tt> and <tt>get</tt> for <tt>add</tt> and <tt>indexAt</tt>. | |||
<code> | |||
... | |||
Hashtable myTable = new Hashtable(); | Hashtable myTable = new Hashtable(); | ||
String addObj = new String("Alpha"); | String addObj = new String("Alpha"); | ||
| Line 399: | Line 300: | ||
Integer tmpInt = (Integer)myTable.get("one"); | Integer tmpInt = (Integer)myTable.get("one"); | ||
String tmpStr = (String)myTable.get("Alpha"); | String tmpStr = (String)myTable.get("Alpha"); | ||
</code> | |||
Note that <tt>put</tt> needs two objects, the key and the value to be stored. Many times the key and the value are the very same object, the object maps to itself. That is not necessary of course, as the <tt> Integer </tt> example shows, the only way to get to the integer object is to give the key "one". That is, the key to "James Bond" may be "Agent 007", no other key will ever reveal the name of that spy. | |||
< | |||
< | With String the <tt>equals</tt> does a compare character by character and does not pay any attention to where the <tt>String</tt> objects actually are stored in memory. Thus you can get to a value by, for example another "Alpha" that in fact is a new <tt>String</tt> object, but still gives the same hash value and equals very well. If, on the contrary, the <tt>Integer</tt> object were put with itself as a key, we need to have it on hand to get it out later and that is not what we liked to. Hence a good practice with your classes may be a good <tt>equals</tt> method, or a good <tt>toString</tt> that produces a known key that you may replicate later on, without need to keep it on hand. | ||
A very, very simple test case. | |||
[[Image:java13h.gif|frame|A hash test drive]] | |||
At least at my computer I found that some of the latter strings produce exactly the same hash value, maybe a flaw in the <tt>hashCode</tt> implementation with very long strings, as the latter strings came to be. Else we understand that the strings produce a hash value that is later used by <tt> put </tt> to insert the strings at their indexes in the hash table array. | |||
We can not get the exact length of that array in the end, but I guess it might be 47 since the default size is 11 (primes gives better result than other sizes) and the default load factor is 0.75. Hence two turns in <tt> rehash </tt> have to be done, each does <tt>size * 2 + 1</tt>. This time we waste more than 50% of the memory foot print, since it was only two or three elements added after the latest rehash, but there is room for 15 elements until the next rehash. | |||
=== | ===Summary=== | ||
We have made a deep and much theoretical dive into the field of data structures. The outcome will be that we have to think twice when we are to chose a structure. Is the look-up time important, or is sortability more important? Is duplicate elements to expect, or should they not be allowed? How limited is the working memory? | |||
The main difference between ordinary arrays and list on the one hand, and maps on the other hand is that the former use an index to get to an element, the latter use the key-value concept. | |||
We will use many of the discussed structures in the future and the next time we will start a slow wandering through streams, reading and writing. And continuing this shock start on data structures, but only one or two types at a time. | |||
Thanks for this time and CU around. | |||
---- | ---- | ||
Note: This columns covers some classes only found in Java 2 or later, some others are also found in Java 1.1.8. The theory holds for anyone. | |||
Also note that Collections (with a trailing s) is the name of the framework, but <tt>Collection</tt> is an interface found in the <tt>java.util</tt> package. | |||
[[Category: | [[Category:Java Articles]] | ||
Latest revision as of 14:55, 21 March 2018
| I | II | III | IV | V | VI | VII | VIII | IX | X | XI | XII |
|---|---|---|---|---|---|---|---|---|---|---|---|
| XIII | IV | XV | XVI | XVII | XVIII | XIX | XX | XXI | XXII | XXIII |
Into Java, Part 13
How amazing, this instalment numbers thirteen and the columns now span over three years and two millennia. Now even the puritans can agree on that, December 31th last year the second millennium ended and the third one started. Time is flying away too fast to imagine, but the computer business seems to keep in pace.
This time we will have a discussion on data structures. Fred Brooks once wrote: "Show me your {code} and conceal your , and I shall continue to be mystified. Show me your , and I won't usually need your {code}; it'll be obvious."--The Mythical Man-Month, Ch 9.
Yes, data structures most often is the heart of your implementation, a good choice will reward you several times over, a bad choice and you will regret it over and over again. That is since data structures quickly becomes the skeleton of your application, and as your skeleton hardly is replaced, data structures are hard to replace.
I have said before that good and thoroughly modelling is essential to programming, using papers and a pencil. But how to include the data structures in that planning. This column will entirely discuss that topic.
Mathematics and computer science go hand in hand, so even this time. Hence I will cover a little maths, but do not be scared off, I will not go too deep into that. Further computer hardware works in its own way, and we have to be aware of a few things because of that.
The developers at SUN seems to have read their maths before implementing the Collections framework in Java 2 (see [#note note]), hence we start with a few maths notations, then how these are implemented in data structures. You may also read the interesting pages in the Java API v 1.2 or later, X/docs/guide/collections/overview.html there you have to substitute X with your folder, or a URL to SUN's site.
The math
A set is simply described as a collection of elements that need not be ordered. The Set interface used in Java follows the hard restrictions that maths states, no two equal elements are allowed. We may think of an alphabet (unordered though), no two equal letters are allowed. On the other hand we are not forced to put every letter we know about in the set, I would hardly put umlaut letters in an alphabet showed to English readers, though I know these letters very well.
The Java Set is an interface that specifies quite a few methods that a set should have, but Java has a class of the Set interface ready to use, the HashSet. Further Set is implemented by the SortedSet interface, that in its turn is implemented by TreeSet. (Please do not be worried by the many class names, we will look to some of them, and the remaining ones you may look up in the Java API.)
A list is on the contrary an ordered collection allowing duplicates. Ordered does not imply sorted, only that we know that item "X" is located at index 45, and maybe another "X" at index 201. Or wherever. Only think of a lined up scout patrol, a straight row there everyone has his/her place in the line, though no need to line up by names and two Bill Smith is allowed.
Java uses the List interface of methods that give us precise control over where we store your objects. We have already used Vector that is an implementation of List, but there are also LinkedList and ArrayList to chose from.
Furthermore, map that is more of a function, as sin(60) maps to 0.5, or telephoneNumber(Gronlund, Simon) maps to 1234567, a key maps to a value. Since a discrete key maps to a discrete value no two duplicate values are allowed. A map is not considered ordered, no straight line of elements is found, nor are they promised to be sorted though some Java classes that follow the Map interface are sorted.
HashMap, Hashtable and WeakHashMap are some classes that implements the Map interface, as well as another interface, the SortedMap that is implemented by TreeMap.
These three fields matches the major interfaces of the Java Collections framework. Java Collection also has the SortedSet, but we will wait with that until another Java column.
root
|
|
node
/ \
/ \
/ \
node node
/ \ / \
/ \ / \
node leaf node leaf
/ \ / \
/ \ / \
leaf node leaf leaf
/ \
A binary tree, two branches out of each node
Finally, I will mention a very useful structure, namely a tree, named so because of its shape. Think of a tree upside down, the root is topmost and the branches grows from the root to the leaves at the end of each branch.
Though many trees used are binary, they have only two branches each node, there are other flavours too. I have used trees with as much as 28 branches each node, but then we are not really discussing ordinary trees and we will leave that for now. Why trees are that popular will be explained in a few minutes but they are, and then binary (and ternary, i.e. 3-branched) trees are the most popular ones.
Trees are a big area of research, included in graph theory, and many interesting results have been found by computer scientists, tailored, used and adopted in the computer industry. Of course trees have found their way into the Java Collection, for example TreeMap, that is a well thought out piece, and its cousin TreeSet, that is something in between.
Before we continue I will introduce a few words, and their meaning. A node is a point in a tree or a list that we may walk to, following a reference. It has at least one reference to it and may have one, two or more references out. Most nodes are made up by a small class, a helper class, that holds the references to 1/ the data, 2/ other nodes whereof one may be the parent node, and 3/ some internal information. Nodes are used on other data structures than trees and works almost the same wherever they are found, as the private and invisible class Entry inside LinkedList is a node.
The non-value null is used when there is no reference to another node, and if every variable that should point downwards to another node is null, this node is considered a leaf, it has data but no legal references.
Accordingly child and parent are used, the child is a node of this node, and a parent is this node's superior level node. These terms may be fuzzy when complex structures are used and no obvious levels or ancestors are seen.
The root is often used as the main class of the particular data structure, and holds a reference to the first node but most often no data. The root holds most of the convenient methods that are used on the data structure, such as add, remove, contains, etc. Since Java gives us many prefabricated methods we may perhaps be happy with numerous of them.
Finally, the way you need to go from the root to a specific node is called path, but in fact any way you need to go in a graph such as a tree is called a path.
Computer basics
From the very beginning technicians have been storing data as bit by bit, normally thought of as 1 and 0, and implemented as distinct electrical values, such as +85mV and -85mV or alike. The bits are held together as a byte, now a byte is thought of as an eight bit byte. Do not confuse a byte with the 32 bit (or 64 bit) compound that is called a word. A word is set up by several eight bit bytes.
| Type | Size | Range (approximately) |
|---|---|---|
| Floating-point numbers | ||
| double | 8 bytes | 1.7977E+308, 15 significant digits |
| float | 4 bytes | 3.4028E+38, 6 significant digits |
| Integer numbers | ||
| long | 8 bytes | 9,223,372,000,000,000,000L |
| int | 4 bytes | 2,147,483,000 |
| short | 2 bytes | 32,768 to 32,767 |
| byte | 1 byte | -128 to 127 |
In one of the first parts of this Java programming series we looked at the basic data types, let us remind ourselves. First we can see that Java is already prepared for easy handling by 64 bit CPU's, as double and long is 8 x 8 = 64 bits long. But the smallest compound, the byte, is one eight bit byte only.
Shall we now think of how data is stored in the computers working memory (RAM). That is not hard to explain, whenever the CPU reads an instruction that tells it to store a variable (let us say an int) it needs two parts, the data and the address in the memory. The latter is made up by the compiler (and the JVM when using Java) in conjunction with the operating system (OS), and the very smallest area to address is an 8 bit byte.
When the CPU executes that instruction it accesses the RAM at the told address and stores the data there. Another variable may later be stored, and is then stored at another address. The more variables stored the more addresses are used, but there are no distinct rule where these addresses may be located. Hence they may be scattered around, or accidentally be grouped together. But no one variable knows the location of the others, they are no part of a data structure.
Arrays--the simplest structure
A long time ago the array was found as a good way to collect related variables together. We may for example measure the temperature each hour and need a way to store these values, then a 24-element array is suitable, one array each day.
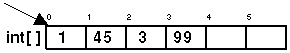
An array is simply several variables in a row, the compiler fixed some kind of code that orders a line of consecutive variables as seen in the image and the OS manages that. The advantage from this is that now we only need one address that points to the beginning of the array, held by the reference.
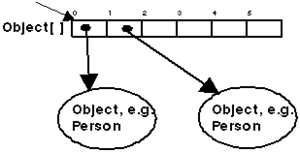
The elements is found as the result from add up the reference with the offset, the first element having zero offset. Here is the reason why arrays, Vector and other data structures start at number zero, the offset is zero at the first element. Hence we now can get to "99" by adding 3 to the reference, as int answer = myIntArray[3] where myIntArray holds the reference.
Arrays may be used not only with basic data types as byte, short, int, long, float or double, yes, in fact, with boolean as well. But we can add any kind of objects to them; MyClass[], Integer[] or Object[] are legal, as any class is. If different kind of objects have to be stored in the same array, then use the cosmic Object class as the type.
Normal array operations are as follows. Please note that arrays have a convenience variable named length that is read directly and not through a method. Also note that arrays always are accessed with square brackets; [ ].
byte[] byteArray; // declaration only
// later, initiation with size 9
byteArray = new byte[9];
/* declaration and initiating of an array of size 17 */
short[] shortArray = new short[17];
/* and using Object, size 5 */
Object[] objArray = new Object[5];
/* declaration and initiating of an array, size becomes 5
* and the elements 1, 2, 3, 4 and 5 are stored in it */
int[] integerArray = {1, 2, 3, 4, 5};
/* and using String, size becomes 3 */
String[] stringStore = {new String("Alpha"),
new String("Beta"), new String("Gamma")};
/* assigning values to an array */
shortArray[0] = 4;
shortArray[17] = 12; // illegal, indexes are 0 to 16, see above
shortArray[10] = 125000; // illegal, >32768, a short's limit
stringStore[0] = new String("Omega");
stringStore[1] = new StringTokenizer("Delta"); // illegal
// StringTokenizer is not a String
/* getting values from arrays */
int x = integerArray[0]; // x will be assigned 1
int y = integerArray[5]; // illegal, index out of bounds
/* and getting objects */
String tempStr = stringStore[2]; // access to Gamma
/* finally try this */
for (int i = 0; i < integerArray.length; i++) {
// set a value in integerArray
integerArray[i] = (i * i); // square of i
}
for (int i = (integerArray.length - 1); i >= 0; i--) {
// get values from integerArray
System.out.println("i = " + i + " and i*i = "
+ integerArray[i]);
}
/* finally set and get values from the objArray */
objArray[0] = new String("zero");
objArray[1] = new Integer(1);
objArray[2] = new Double(2.0);
objArray[3] = new Character('3');
String newStr = (String)objArray[0]; // cast is needed
Integer newInt = (Integer)objArray[1];
...
Using arrays is convenient, and as they are very close to the computer hardware environment they are efficient and do not cause that much overhead. Why not only using arrays then?
The first limitation is the length of an array. The length can not be changed dynamically, and that is true for every kind of computer and OS, always. If any programming language looks like having such a feature, that is a fake, beneath the surface there is some kind of functionality fooling us around. That is clearly understood when considering how an array is laid out, the OS gets an order for, let us say, an int sized array with 10 elements. That is 10 by 4 bytes (an int needs 32 bits and 4 bytes * 8 bits = 32 bits) resulting in 40 bytes in a row. Maybe next step for the OS is an order for one long sized variable (8 bytes) and by an unlucky coincidence it is placed at the very next free address after the array. Thus the array can not grow into that spot.
Growing an array is a simple matter of ordering a new one, that much longer as we like it to be. The OS will give us a new and empty one and we then do a simple copy and paste from the original to the latter one using arrayCopy of the System class. Finally we simply leave the original to destruction and soon the OS will recycle the address area. Exactly the same operation is performed upon shrinking the length. These operations are of course time consuming and considered inefficient. Still many Java classes are based on simple arrays, as Vector uses an Object array and performs the operations just explained when necessary.
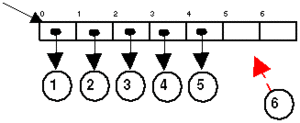
Else, normal actions on simple arrays are performed efficiently and with no hassle. They are easily understood and not hard to implement. Since Java hides the hazards with pointers and pointer arithmetic the work is a breeze, as the add method show us in the left hand image. We simply keeps track of the last index used and add the next element to the next index.
The next inconvenience occurs when we implement the remove and insert methods, let us discuss them to some extent. The simple removeLast and insertLast are disregarded as they are implemented as decrementing the size variable and add respectively.
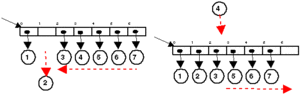
Consider the left part of the image, we remove the second element. Remove is clearly different from assigning the second box another object, remove will leave an empty box, and empty boxes, how would you like to keep track of them? You don't, you have to move every element to the right of the empty box one step leftward. Again that is time consuming, more time is spent the more leftward the removed element was located and the longer the array is.
Exactly the same argument is valid with insert, we have to move every element to the right one step rightward, finally we can add the new element in the obtained empty box. Both methods have the worst case scenario of T( n ) where n is the number of elements in the array and T is the time spent on each iteration (computer scientists use the term big-O, but we will leave that). The best case is T( 1 ) since that is simply removeLast or insertLast discussed earlier. The average case is T( n /2 ) since the average case is the middle element being changed. To that we most of the times have to add the time to find which index the element we will remove has, or the one to insert is to be given, which doubles the time.
Hence arrays and classes that are built on arrays are good for simple data structures without too many remove or insert. Order an array of the expected length from the very beginning, thus avoiding too many arrayCopy operations. Many delicate implementations are built on simple arrays. On the other hand many applications suffer from being built on arrays that do not scale well or suffer from time consuming operations.
Linked lists--the solution to insert and remove cons
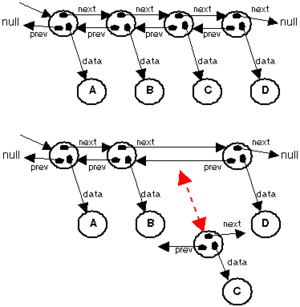
As the problem with insert and remove came from the time spent on arrayCopy, shuffling elements left- or rightward, we would like a data structure that do not need these operations. A linked list is the answer. Think of nodes linked, or chained, together as the uppermost image part shows.
The root knows at least the first node, many times it also knows the last node. If the list is single linked only the next reference is used and we can only traverse the list in one direction, going forward. If the previous reference is used we have a double linked list and can traverse it both ahead and back, as the image shows. The Java LinkedList is a double linked list, also knowing its last node, but note that it is the base class that knows the start and end of the chain, the nodes themselves know only the next and previous, as well as their data.
Now look at the lower part of the image, an insert (or is it a remove?) is to be done. The methods need to change the next and previous references to include (or exclude) the "C" node, that is all. Okay then, that is a little tricky but it is nothing more than switching references so that the "C" node's next will refer to the same as the "B" node does, then changing the next of "B" to refer to the "C" node (note that we talk about the nodes and not the data, but use the data as a label in our discussion). Likewise we set the previous of the "C" node to reflect the "D" nodes reference, and then changes the previous of the "D" node to refer to "C". The remove is analogous to this procedure.
Hey presto, now both insert and remove will only take T( 1 ) since there is no shuffling elements around. The different objects may be stored anywhere in the computers RAM, still the variables refer to the correct objects. But are there no drawbacks?
Of course there are some drawbacks and some shortcomings, every data structure suffers from limitations and you are the one to chose the best compromise. Handling arrays are efficient in many ways, the data is stored tight to each other and hence derive advantage from the "read-ahead" that most OS's use, from the cache mechanism and a few more benefits. Instantiating objects eats time, we never know were they actually are stored (we do not need to, but the tight data storage is lost) and there is some overhead with objects.
Anyway, quite a few times we decide that we can live with these shortcomings, the usefulness outweighs the shortcomings. But still the worst thing is that methods like contains(Object) or remove(Object) still have the same best, average and worst cases. How come? Since these methods have to iterate each node until the correct data is found. There is no shortcut to find the correct one, each one has to be examined with a fail or pass.
The same arguments hold if we like to maintain a sorted list (Java LinkedList do not support sortability, but we are free to implement such a list). To sort a "Y" after "X" we have to find "X", and that takes T( n /2 ) on average.
Lists are mainly used to hold queues, methods like addFirst and removeFirst performs well and the overhead is ignorable in these cases. Unordered collections perform well, except from searching them.
Now we have tracked down to "how to sort into a sorted data structure?" So far we have found no good data structure to maintain a sorted collection and perform operations on that collections efficiently, though the linked list is much better than an array. Any kind of array or list suffers from being linear, it is traversed ahead or backwards. May the tree structure be the solution?
The binary tree
Straight to the point, the tree is outstandingly fast with insert, remove, contains(Object) and whatever we like to process on it. Trees belong under set discussed as the first of three math definitions, a set do not allow duplicate objects stored.
If we consider a huge telephone database, there is not two objects referring to the one individual. If so, the database will soon get unstable and when we update one record the other one will still be reflecting old data. Fulfilling these requirements of no duplicates we can start with instantiating MyTree, that is we get ourselves a root to the still not yet created first node.
We pick the first individual and instantiate an object from the data read. Then we pass the data to add(Object) that creates a new node referring to the object. Since it is the first node added to the tree it simply becomes the first node the root refers to, and the node itself have only two null-references as the left and right variables. The value of the data is so far irrelevant.
Next individual is instantiated and the object is passed to add(Object) that creates a new node. But since it is not the first node added to the tree we have to find out if it is to be placed to the left or the right from the existing node, using the left or right child of the first node. To make that comparison our object must be able to answer a compare-to question, that is, we have to have a method named compareTo. That method is outlined in the Comparable interface that we have to implement in our class if we are using any of the Java Collections' classes that support sorted collections.
compareTo(Object)
A class implementing the Comparable interface only has to implement the single compareTo(Object) method. Think of us standing in an object, the this object. We receive another object, named other, and we have to answer to the question "is the other object lesser than, equal to, or bigger than your object is?" Look at the limited code below.
public class MyShoes implements Comparable {
short shoeSize;
public MyShoes(short size) {
shoeSize = size;
}
public int compareTo(Object other) {
MyShoes temp = (MyShoes)other; // a cast
return (int)(temp.shoeSize - this.shoeSize);
}
}
Naturally other things may guide the comparison of shoes than only the size, but the lesson is the same. We return a negative int value if we are less than the other object, zero if we are equally sized, or a positive int if we are bigger than the other. For example, the String class performs a true lexicographically comparison, taking upper and lower cases into account. How we compare objects is up to us, but the comparison has to be done if we like to maintain a sorted collection.
Continuing with the adding to the tree we chose left or right, less than to the left, else to the right (equal to is not allowed). This time we imagine we got the left choice. Reading the third individual results in the next node, which data shall be compared with the first node's data, left or right. If it is to the left we continue with comparing the new node with the left node's data, the second node made. That is, we have to go one step deeper to make another comparison. Else we can simply add the new node as the right child to the first node. I will try to illustrate it.
I. root II. root III. root IV. root V. root
| | | | |
"Mike" "Mike" "Mike" "Mike" "Mike"
/ / / / \
"John" "John" "John" "John" "Simon"
/ / \ / \
"Chris" "Chris" "Len" "Chris" "Len"
For example "Chris" is first compared to "Mike", then to "John" and is then set as the left child of "John", but "Len" is lesser than "Mike" but greater than "John" and was set to the right of "John". But this tree does not look sorted at first sight, does it? Reading a tree in order we first have to find the leftmost node, in our case "Chris" that also is the first name of this collection. From that node one step up to the parent and reading that node, "John", which is correct. Then down the right child one level, and try to find the leftmost node again (which can be a few levels down actually). This time there is no leftmost node of that child so we read the node, "Len", again correct. Try to go down to the right, but there is no right child. Upwards, but we have read John so we leave him and head for his parent, "Mike", that is correct. Does "Mike" has a right child? And does that child has a leftmost node downwards? "Mike" has a child, "Simon", which has no children. We are done.
The rules seems to be,
- try to go left
- if possible, go there and continue from 1
- else, continue with 2
- read this one
- try to go right
- if possible, go there and continue from 1
- else, do nothing, we will recursively return to your parent
and we will get the elements in a sorted way. The recursion is the tricky part to follow, but remember that the computer remembers were it left off for the child, and the parent will continue executing the code were it left off for a while. Since there are such advanced and good Java classes prefabricated I will not give any code here, only links to the recursion instalments, Part V and Part VI that explains the mechanism used.
Now, why use such non trivial structures as trees? Since they give an outstanding performance hit on sorted collections, any kind of look-this-up operation is done fast and quickly, if the object is in the tree it is found that snappily, or it says "the object is not found". Insert-this is executed as quickly. How come?
Here a little more maths is needed. The example above is not that big, but still it shows that each level double the number of nodes, the zero level is only one node, the first level is two of them, "John" and "Simon". The second level is already having place for four nodes, though only two is used. The next level will have eight, the next sixteen and so forth. Clearly we see n = 2h where n is the number of nodes possible, and h is the height of the tree, the number of levels used, having the first node at level zero. But that is not the whole truth, since each node at each level also may be used and that gives a much better sum of nodes, an expression that reads n = 2(h+1) - 1.
Such expressions grow rapidly, only ten levels, including the zero level, will give room for 1,023 nodes, and 20 such levels will gladly accept more than one million objects. Hence I can promise that a telephone number database with one million individuals will never suffer from more than T(20), or more precisely put, the worst case will be T(h), where h may be computed by h = lg(n). But this is not completely true, since that is based on the assumption that all trees grow balanced and equally, which is not a fact. Still the Java classes that support sorted trees are that close to the lg(n) that we can forget about the difference.
There is simply no other data structure giving us this splendid performance with that little implementation effort, we can find any person of that one million person telephone database within 20 comparisons, remove him or simply read the data. An insert is made equally fast. Is there any drawbacks then?
Yes, of course there are drawbacks, didn't I told you? <grin> So far we assumed that the input to the tree was picking individuals randomly, but consider moving from one ordered and sorted data structure, that have served for a while, to a tree. We pick the first individual, "Aaron", then comes "Abel", "Abdul", and so forth. "Aaron" will of course be the first and topmost node, but "Abel" will surely be bigger than him and set as the right child. So will "Abdul", "Abraham" and every other individual be, set as the right child to the right child, no one will ever be placed to the left. The result is again a linked list and the last person will be that many levels away from the root.
Apparently a tree is not suited for that kind of input, but else it works nice. There are naturally several ways to solve the dilemma, pick the objects at random and watch out for picking the same twice and not to forget someone, or start at the middle and then recursively pick the elements as in the recursions discussed in instalment 6. Or any other method of your mind.
To avoid heavy unbalance in trees something named the red-black tree was invented and implemented, in fact it is used by Java TreeMap. It promises that no path is more than twice as long as any other path, thus giving us a reasonable balanced tree. Consider that the more precise balancing we require the more overhead it causes the tree's balancing mechanism. And there is not much difference between 10 and 20 levels, not compared to the up to one million look-ups on a list or array, or 500,000 on average.
The map, hash and table
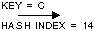
Still the data structures we have examined do not have T(1) at look-ups. Is there a way to get such good results? Yes, the mapping concept gives that performance. Consider having an array with 30 empty indexes, and a function that takes the object, or a key, and computes something (a pseudo-index) that can be mapped to an index of were to put the object. If that function promises to always compute the same pseudo-index from equal keys, and also to spread these pseudo-indexes equally along over a fix length, then any look-up or insert will execute with T(1). This data structure is mainly called hash table or hash map since we hash the pseudo-index, called the hash value, from the key. That hash value is mapped into an index of the array and the object is put in a table or a map. Are there any drawbacks <grin>?
Collisions, when it happens that two unequal keys gives the same index (rare but possible), cause a drawback that gives us some headache, we have to take care of the situation and that will increase the time consumed somewhat. Another drawback is the same as with arrays, if the table grows to much we have to lengthen the array. But we cannot use the speedy arrayCopy, instead we have to re-hash (re-map the hash values) of every object since now we have more indexes to chose from and the look-up function will map the hash value onto that many indexes, not onto the previous length. This re-hashing wastes a lot of time, but can be prepared for by giving the table a good initial size.
Also, to avoid too many collisions we must waste some memory, some unused memory. The benefit is that the mapping will be wider or broader and thus the chance is better that a collision will not occur. It is not correct, but simple, to say that there are more free slots to pick from. Incorrect since the mapping does not use the free/not-free state in its calculation of the index. But it is simple since the more free slots there are the better chance to get a free one. Normally a hash table uses a load factor of 0.75, it wastes at least 25% memory space, "a good trade-off between time and space costs" as the Java API states.
Finally the default hash table does not allow duplicate objects, that is since the hash function will produce the very same hash value again and if there is no way to tell two identical objects apart, how will the computer do then? Adding two "John Smith" objects will not be good, but maybe there are two such persons but they have different addresses, birth date etc., that can be used by the hash function too.
Or, better, we have to follow the rule that says that we should have an equals(Object) method in your added object. That is, we have to implement a method that can tell apart different objects, even though they look alike, and return a boolean true or false. There is an equals(Object) in the Object class, but that can only tell apart objects that are truly stored at different locations of your RAM, it does not compare them on a more solid basis. Hence, if we by mistake make two objects based on the same person, or whatever, they are considered not-equal by that method, though they in real life are one.
put and get
Since mapping structures have that nice performance they are used quite often. But the way to use them differs from the previous structures that used a simple add(Object) method. First we have to implement the two methods mentioned, hashCode and equals, both described in the Object class. (Sometimes the methods of Object is sufficient, then we are done.)
Unfortunately the description on hashCode does not tell the range of the int to return. Do not worry, any valid integer is okay. The hard thing with hashCode is to find out how to equitable spread out the result. The best case is when two distinct objects, differing only by a fraction, are not given hash values close to each other (guess if there is much toil spent on finding good hash functions). Given the hash value the table will compute it into an appropriate index based on the tables actual size and the load factor wished, and finally add the object somewhere in the array.
The equals(Object) method is still the heart of the hash table functionality. It is up to us to decide the basis for equality. If we are sure that no two objects will be instantiated from the same source (e.g. a person), we can rely on the Object class. Else we have to think about how to tell objects apart, and return a true or false.
Next step is described in the code below. Notice that we do not make any use of the hashCode or equals methods, but the table does. Since the Java Hashtable follows the Map interface we use the two methods put and get for add and indexAt.
...
Hashtable myTable = new Hashtable();
String addObj = new String("Alpha");
myTable.put(addObj, addObj);
addObj = new String("Beta");
myTable.put("Beta", addObj);
myTable.put("one", new Integer(1));
Integer tmpInt = (Integer)myTable.get("one");
String tmpStr = (String)myTable.get("Alpha");
Note that put needs two objects, the key and the value to be stored. Many times the key and the value are the very same object, the object maps to itself. That is not necessary of course, as the Integer example shows, the only way to get to the integer object is to give the key "one". That is, the key to "James Bond" may be "Agent 007", no other key will ever reveal the name of that spy.
With String the equals does a compare character by character and does not pay any attention to where the String objects actually are stored in memory. Thus you can get to a value by, for example another "Alpha" that in fact is a new String object, but still gives the same hash value and equals very well. If, on the contrary, the Integer object were put with itself as a key, we need to have it on hand to get it out later and that is not what we liked to. Hence a good practice with your classes may be a good equals method, or a good toString that produces a known key that you may replicate later on, without need to keep it on hand.
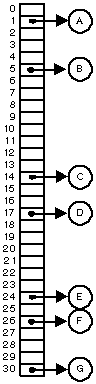
A very, very simple test case.

At least at my computer I found that some of the latter strings produce exactly the same hash value, maybe a flaw in the hashCode implementation with very long strings, as the latter strings came to be. Else we understand that the strings produce a hash value that is later used by put to insert the strings at their indexes in the hash table array.
We can not get the exact length of that array in the end, but I guess it might be 47 since the default size is 11 (primes gives better result than other sizes) and the default load factor is 0.75. Hence two turns in rehash have to be done, each does size * 2 + 1. This time we waste more than 50% of the memory foot print, since it was only two or three elements added after the latest rehash, but there is room for 15 elements until the next rehash.
Summary
We have made a deep and much theoretical dive into the field of data structures. The outcome will be that we have to think twice when we are to chose a structure. Is the look-up time important, or is sortability more important? Is duplicate elements to expect, or should they not be allowed? How limited is the working memory?
The main difference between ordinary arrays and list on the one hand, and maps on the other hand is that the former use an index to get to an element, the latter use the key-value concept.
We will use many of the discussed structures in the future and the next time we will start a slow wandering through streams, reading and writing. And continuing this shock start on data structures, but only one or two types at a time.
Thanks for this time and CU around.
Note: This columns covers some classes only found in Java 2 or later, some others are also found in Java 1.1.8. The theory holds for anyone.
Also note that Collections (with a trailing s) is the name of the framework, but Collection is an interface found in the java.util package.